Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
檜作 響子*; 藤淵 俊王*; Han, D.*; 荒川 弘之*; 古田 琢哉
Radiological Physics and Technology, 18(1), p.196 - 208, 2025/03
X線透視業務に携わる医療従事者の放射線防護対策一つとして放射線防護板の使用があり、効率的な防護板による遮蔽を検討するためのシミュレーションツールの開発が求められている。モンテカルロシミュレーションはX線とX線室内に存在する様々な物質との相互作用を非常に精度良く計算できる一方で、計算時間がかかり過ぎるという欠点があるため、放射線防護板の影響を短時間で見積もる目的に、事前計算された方向ベクトルを用いて短時間に線量分布を計算する簡易線量分布計算法を新たに開発した。まず、放射線防護板が存在しない状態でのX線室内の線量分布をモンテカルロシミュレーションコードPHITSを用いて計算し、X線室内をグリッドに分割した線量分布と各位置における方向ベクトル分布を取得する。開発した簡易線量分布計算法では、グリッド位置における線量はその位置での方向ベクトルの指し示す方向からの放射線により全て付与されるものと仮定し、方向ベクトルを逆方向にトレースした方向に放射線防護板が存在する場合には、そのグリッド位置での線量値は防護板による遮蔽効果を受けるものとして線量分布を計算する。この手法を用いることで、効率的な防護板の配置を検討する上で十分な精度を保ちつつ、PHITSで全計算を実行するのに比べて、計算時間を1/6000に短縮することに成功した。
鈴木 喜雄; 松本 伸子*; 山岸 信寛*; 荒川 拓也*; 倉石 英明*
JAERI-Data/Code 2004-013, 163 Pages, 2005/02
日本原子力研究所計算科学技術推進センターでは、e-Japan重点計画の一つであるITBL(Information-Technology Based Laboratory)計画を推進している。ITBL計画の目的は、大学や研究機関に分散された計算機・プログラム・データ等の知的資源を共有し、研究者間の共同研究を支援するための仮想研究環境の構築である。AVS/ITBLは、このITBL環境において効率的に可視化が行えることを目指して開発している可視化ツールである。本可視化ツールは、ITBL基盤ソフトウェア上のツールとして実装しており、AVS/Expressと連携して動作する。AVS/ITBLの主な機能として、ITBL環境において遠隔地にある計算データを直接的に可視化可能なAVSクライアントによる可視化機能,Webブラウザで可視化画像を表示可能なWebクライアントによる可視化機能,複数の利用者が協調して可視化を行うことが可能な可視化コラボレーション機能、及びシコマンドラインからの実行によりバッチ的に可視化を行うことが可能なバッチ可視化機能がある。本書では、ITBL計画におけるアプリケーションの一つである数値環境システムでのこれら機能の利用手引について記述しており、操作概要について詳細に記述を行っている。
上島 豊; 荒川 拓也*; 佐々木 明; 横田 恒*
JAERI-Data/Code 99-051, p.23 - 0, 2000/01
日本で100並列を越える並列計算が、実際に行われるようになったのは、つい数年ほど前からである。日本原子力研究所(原研)のIntel製Paragon XP/S 15GP256 那珂研究所
那珂研究所 、75MP834
、75MP834 関西研究所
関西研究所 は、本格的超並列計算機の先駆けとして光量子、核融合の大規模、超並列計算を目的に導入されている。これらの計算機を使って超並列計算を行うためは、多くの超並列計算プログラムが移植や新規作成されている。これらのプログラムは、従来、ワークステーションやベクトル計算機上で動作していたものをそのまま移植したものか、並列用にアルゴリズムの変更を施したものである。異なる計算機及びオペレーティングシステム(OS)のもとでのプログラム開発には、細心の注意とノウハウが必要であるが、Paragonに到ってはユーザ数が極めて少ないため、ノウハウの集積と環境の標準化が大変困難な状況にある。原研関西研究所におけるParagon XP/S 75MP834上での超並列計算プログラム開発において得た情報をParagon上でのスカラー超並列プログラム開発ガイドとしてJAERI-Data/Code 98-030にまとめた。本報告書では、超並列計算機が持つ特殊性が際立つ入出力周りにテーマを限定して、より高速かつ安定に入出力を実行できる方法をFortranとCのプログラム実例入りで解説する。
は、本格的超並列計算機の先駆けとして光量子、核融合の大規模、超並列計算を目的に導入されている。これらの計算機を使って超並列計算を行うためは、多くの超並列計算プログラムが移植や新規作成されている。これらのプログラムは、従来、ワークステーションやベクトル計算機上で動作していたものをそのまま移植したものか、並列用にアルゴリズムの変更を施したものである。異なる計算機及びオペレーティングシステム(OS)のもとでのプログラム開発には、細心の注意とノウハウが必要であるが、Paragonに到ってはユーザ数が極めて少ないため、ノウハウの集積と環境の標準化が大変困難な状況にある。原研関西研究所におけるParagon XP/S 75MP834上での超並列計算プログラム開発において得た情報をParagon上でのスカラー超並列プログラム開発ガイドとしてJAERI-Data/Code 98-030にまとめた。本報告書では、超並列計算機が持つ特殊性が際立つ入出力周りにテーマを限定して、より高速かつ安定に入出力を実行できる方法をFortranとCのプログラム実例入りで解説する。
上島 豊*; 荒川 拓也*; 岸本 泰明; 佐々木 明; 田島 俊樹*
Inst. Phys. Conf. Ser., (159), p.325 - 328, 1999/00
今年の3月に原研が達成した100TW、20フェムト秒の短パルス相対論的高強度レーザーを低Z物質に照射すると、レーザーパルス長程度の短パルスX線が発生することが期待される。このX線放射の主要なメカニズムは、ラーマー放射と制動放射であり、それぞれkeV、MeVを越えるエネルギーの極短パルス高強度X線を発生する。われわれは、このX線放射の強度、放射角度分布、光子エネルギースペクトラムを明らかにするために、1G粒子を使った大規模2次元PICコードによりシミュレーションを行った。また、このシミュレーションによりターゲットの電子密度、レーザーの集光、イオン化、衝突過程がX線生成過程にどのような影響を及ぼすか、また、ほかの競合現象との関係について考察し、発生しうる短パルスX線の応用についていくつかの提案を試みる。
上島 豊*; 荒川 拓也*; 佐々木 明; 横田 恒*
JAERI-Data/Code 98-030, 69 Pages, 1998/10
ここ4,5年前までは、最も高速な計算機といえば、いわゆるスーパーコンピュータと呼ばれるベクトル型計算機であった。この型の計算機は4,5年で計算速度が10倍ずつ高速になってきた。しかし、現在、1CPUの演算速度が限界に達してきている。日本でこれを超える計算機として100並列を越える並列計算機が、実際に行われるようになったのは、つい数年前ほどからである。日本原子力研究所(原研)のIntel製Paragon XP/S 15GP256 那珂研究所(那珂研)
那珂研究所(那珂研) 、75MP834
、75MP834 関西研究所(関西研)
関西研究所(関西研) は、このような計算機の先駆けとして光量子、核融合の大規模超並列計算を行う目的に導入されている。これらの計算機を使って超並列計算を行うために、多くの超並列計算プログラムが移植や新規作成されている。しかし、超並列計算機に関しては、ユーザ数が極めて少ないため、ノウハウの集積と環境の標準化が大変困難な状況にある。そのため、原研関西研究所におけるParagon XP/S 75MP834上での超並列計算プログラム開発において得た情報をParagon上での超並列プログラム開発の指針としてまとめた。
は、このような計算機の先駆けとして光量子、核融合の大規模超並列計算を行う目的に導入されている。これらの計算機を使って超並列計算を行うために、多くの超並列計算プログラムが移植や新規作成されている。しかし、超並列計算機に関しては、ユーザ数が極めて少ないため、ノウハウの集積と環境の標準化が大変困難な状況にある。そのため、原研関西研究所におけるParagon XP/S 75MP834上での超並列計算プログラム開発において得た情報をParagon上での超並列プログラム開発の指針としてまとめた。
桜井 聡; 荒川 拓也*; 奥野 浩
Journal of Nuclear Science and Technology, 35(5), p.365 - 369, 1998/05
被引用回数:0 パーセンタイル:0.00(Nuclear Science & Technology)均質硝酸プルトニウム溶液体系の無限中性子増倍率(k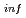 )に与える有機溶媒の影響をMNCP-4Aを用いた数値計算によって調べた。その結果、硝酸プルトニウム-30vol%リン酸トリブチル-ドデカン有機溶媒系のk
)に与える有機溶媒の影響をMNCP-4Aを用いた数値計算によって調べた。その結果、硝酸プルトニウム-30vol%リン酸トリブチル-ドデカン有機溶媒系のk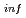 は硝酸プルトニウム水溶液系のk
は硝酸プルトニウム水溶液系のk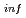 とほぼ等しいことを確認した。しかし、結果をより子細に眺めると、有機溶媒系のk
とほぼ等しいことを確認した。しかし、結果をより子細に眺めると、有機溶媒系のk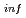 は70gPu/l以下では水溶液系の対応値よりも僅かに大きくなった。それゆえ、
は70gPu/l以下では水溶液系の対応値よりも僅かに大きくなった。それゆえ、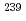 Pu(NO
Pu(NO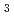 )
)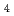 水溶液系の推定臨界下限濃度が6.9g
水溶液系の推定臨界下限濃度が6.9g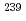 Pu/lであるのに対して、有機溶媒系の推定臨界下限濃度は6.8g
Pu/lであるのに対して、有機溶媒系の推定臨界下限濃度は6.8g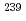 Pu/lとなった。また、有機溶媒系のリン酸トリブチル濃度が上昇するとk
Pu/lとなった。また、有機溶媒系のリン酸トリブチル濃度が上昇するとk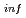 が増加する傾向も見出した。
が増加する傾向も見出した。
桜井 淳; 山本 俊弘; 荒川 拓也*; 内藤 俶孝*
日本原子力学会誌, 40(5), p.380 - 386, 1998/00
被引用回数:0 パーセンタイル:0.00(Nuclear Science & Technology)TCAで実施された二分割結合炉心実験の解析をMCNP 4Aで行った。中性子増倍率の誤差は、筆者らによって提案された「計算誤差間接推定法」で評価した。パルス中性子法シミュレーション計算は17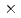 17+5G+17
17+5G+17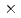 17体系に対して、指数実験法シミュレーションの計算は16
17体系に対して、指数実験法シミュレーションの計算は16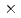 9+3G+16
9+3G+16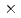 9体系及び16
9体系及び16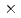 9+5G+16
9+5G+16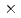 9体系に対して行った。「計算誤差間接推定法」による評価によれば、MCNP 4Aで計算した中性子増倍率には、0.4~0.9%の誤差が見込まれる。従来のパルス中性子法及び指数実験法では中性子増倍率に6%の誤差が見込まれているが、「計算誤差間接推定法」による計算値を用いた未臨界度の評価ではそれを1%以下にできる。
9体系に対して行った。「計算誤差間接推定法」による評価によれば、MCNP 4Aで計算した中性子増倍率には、0.4~0.9%の誤差が見込まれる。従来のパルス中性子法及び指数実験法では中性子増倍率に6%の誤差が見込まれているが、「計算誤差間接推定法」による計算値を用いた未臨界度の評価ではそれを1%以下にできる。
桜井 淳; 山本 俊弘; 荒川 拓也*; 内藤 俶孝
Journal of Nuclear Science and Technology, 34(6), p.544 - 550, 1997/06
被引用回数:2 パーセンタイル:22.80(Nuclear Science & Technology)転水減速・反射、低濃縮UO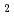 燃料格子炉心での未臨界実験に「計算誤差間接推定法」を適用して未臨界度を推定した。即発中性子減衰定数と空間減衰定数の二つの測定可能な量をMCNP 4AとJENDL-3.2を用いて計算し、その誤差から「計算誤差間接推定法」により反応度とのバイアスを求めた。空間減衰定数の計算値と測定値との差は、実験値の誤差とほぼ同等であった。これにより、MCNP 4AおよびJENDL-3.2を用いた未臨界推定精度は、指数実験で達成可能な精度の範囲内であると言える。一方、計算および測定で求めた即発中性子減衰定数の差から、計算で求めた反応度のバイアスは有意な値が得られた。このバイアス値より計算で求めた実効増倍率に対して補正を行い、未臨界度を推定した。
燃料格子炉心での未臨界実験に「計算誤差間接推定法」を適用して未臨界度を推定した。即発中性子減衰定数と空間減衰定数の二つの測定可能な量をMCNP 4AとJENDL-3.2を用いて計算し、その誤差から「計算誤差間接推定法」により反応度とのバイアスを求めた。空間減衰定数の計算値と測定値との差は、実験値の誤差とほぼ同等であった。これにより、MCNP 4AおよびJENDL-3.2を用いた未臨界推定精度は、指数実験で達成可能な精度の範囲内であると言える。一方、計算および測定で求めた即発中性子減衰定数の差から、計算で求めた反応度のバイアスは有意な値が得られた。このバイアス値より計算で求めた実効増倍率に対して補正を行い、未臨界度を推定した。
山本 俊弘; 桜井 淳; 荒川 拓也*; 内藤 俶孝
Journal of Nuclear Science and Technology, 34(5), p.454 - 460, 1997/05
被引用回数:5 パーセンタイル:42.36(Nuclear Science & Technology)体系の未臨界度を推定するために、「計算誤差間接推定法」という新しい手法を提案する。直接測定の出来ない実効増倍率の「測定値」とその計算値とを比べるのではなく、未臨界実験で測定可能な量の測定値と計算値とを直接比べることで実効増倍率の計算値のバイアスを見積もる。未臨界計算の精度は、これらの測定可能な量の誤差から間接的に導かれる。ここでは、中性子源増倍法、パルス中性子法、指数実験法に基づく三つの推定法を示す。この三つの手法について、それぞれ中性子計数率分布、即発中性子減衰定数、空間減衰定数が計算と推定で比較され、実効増倍率の計算値のバイアスが導かれる。この「間接推定法」により得られたバイアスを用いることで、実効増倍率の「測定値」よりもより高精度に、また、より高い信頼度で体系の未臨界度の推定が可能となる。
酒井 友宏*; 小室 雄一; 荒川 拓也*
JAERI-Data/Code 97-004, 46 Pages, 1997/03
本書は臨界条件データベースの使用マニュアルである。臨界条件データベースの中には、我が国及び諸外国の臨界安全ハンドブック等に記載されている多数の臨界・未臨界データが保存されている。必要な臨界データを簡単に検索できると共に、異なる臨界安全ハンドブックの臨界データの比較図を描くこともできる。このデータベースは、パーソナルコンピュータマッキントッシュ上で稼働するリレーショナル型データベースソフトウェア4th Dimensionを利用している。さらに、臨界データの図を描くためには、適当なグラフィックソフトウェア(例えばKaleida Graph)が必要である。
山本 俊弘; 桜井 淳; 内藤 俶孝; 荒川 拓也*
Proc. of Topical Meeting on Criticality Safety Challenges in the Next Decade, 0, p.365 - 370, 1997/00
計算によって求まるk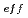 のバイアスを求めるべく、計算誤差間接推定法を提案してきた。この手法は、測定可能な物理量の計算誤差から反応度のバイアスといった測定できない量を推定しようというものである。ここでは、バイアスを推定する量として即発中性子減衰定数を選んだ。MCNPを使って、即発中性子減衰定数をパルス中性子法とFeynman-
のバイアスを求めるべく、計算誤差間接推定法を提案してきた。この手法は、測定可能な物理量の計算誤差から反応度のバイアスといった測定できない量を推定しようというものである。ここでは、バイアスを推定する量として即発中性子減衰定数を選んだ。MCNPを使って、即発中性子減衰定数をパルス中性子法とFeynman-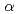 法とから求めた。Feynman-
法とから求めた。Feynman-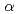 法のシミュレーションを行うためMCNPに対して修正を行った。両者の手法とも特に未臨界度の大きい体系に対しては高次モードの除去が必要となる。パルス法のシミュレーションの方がFeynman-
法のシミュレーションを行うためMCNPに対して修正を行った。両者の手法とも特に未臨界度の大きい体系に対しては高次モードの除去が必要となる。パルス法のシミュレーションの方がFeynman-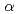 法のそれよりも良い手法であることが判明した。
法のそれよりも良い手法であることが判明した。
桜井 淳; 荒川 拓也*; 山本 俊弘; 小室 雄一; 須崎 武則; 大友 正一; 新田 一雄*; 堀木 欧一郎*
JAERI-Research 96-067, 41 Pages, 1996/12
原研のTCA炉心の中心領域に核分裂生成物核種(B:4濃度、Rh:6濃度、Cs:5濃度、Nd:6濃度、Sm:7濃度、Eu:7濃度、Gd:7濃度、Er:7濃度)を含む体系を構成して中性子断面積積分評価用臨界実験を実施した。それらの体系の厳密な個数密度を算出した。その値を使用して中性子増倍率をMCNP 4AとJENDL-3.2の組合せで計算した(ただし天然Erについては評価済み断面積が世界のどのライブラリーにも存在しないため除外してある)。計算で求めた中性子増倍率は、臨界固有値を非常によく再現している。このことからJENDL-3.2に収納されているこれらの核種の中性子断面積は評価精度がよいと判断される。今回の実験及び解析結果から、ここで取り上げた体系は、FP核種の中性子断面積積分評価用ベンチマーク問題としてすぐれていることが分かった。
桜井 淳; 荒川 拓也*; 山本 俊弘; 内藤 俶孝
JAERI-Research 96-045, 31 Pages, 1996/08
「計算誤差間接推定法」では未臨界度予測精度は、
 -
-
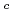 =K(
=K(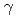
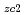 -
-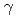
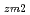 )で表される。この式は、未臨界度予測精度は軸方向のバックリングの予測精度である(
)で表される。この式は、未臨界度予測精度は軸方向のバックリングの予測精度である(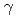
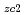 -
-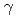
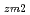 )に比例することを意味している。比例定数Kは計算によって求めるが、Kの不確かさが未臨界度予測精度に与える影響は、直接
)に比例することを意味している。比例定数Kは計算によって求めるが、Kの不確かさが未臨界度予測精度に与える影響は、直接
 =K(
=K(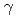
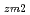 +
+
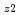 )によって求めた未臨界度と固有値計算によって求めた
)によって求めた未臨界度と固有値計算によって求めた
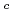 とを比べる場合に比べてはるかに小さい。したがってKの値は、既算の値を計算によって求めておけば精度は充分に保たれる。もし
とを比べる場合に比べてはるかに小さい。したがってKの値は、既算の値を計算によって求めておけば精度は充分に保たれる。もし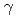
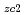 =
=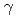
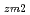 であれば、
であれば、
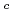 =
=
 となる。TCAの四つの未臨界炉心の実験解析を基にこの方法の信頼性を示すことができた。
となる。TCAの四つの未臨界炉心の実験解析を基にこの方法の信頼性を示すことができた。
桜井 淳; 荒川 拓也*; 内藤 俶孝
JAERI-Research 96-008, 77 Pages, 1996/02
臨界集合体TCAを利用して7種類の未臨界炉心を構成し、反応度と中性子計数率空間分布を測定した。実験解析にはMCNP-4Aを利用した。中性子計数率空間分布の計算結果は、すべてその実測値と相互の誤差範囲内でよく一致している。このことは「計算誤差間接推定法」では、MCNP-4Aでの固有値問題の計算で求めた中性子増倍率は、その体系で実験的に評価した反応度から求めたものに一致することを意味している。今回の実験と計算によって「計算誤差間接推定法」を適用した計算値を用いた未臨界度の評価法の基礎技術を確立することができた。
内藤 俶孝; 山本 俊弘; 荒川 拓也*; 桜井 淳
PHYSOR 96: Int. Conf. on the Physics of Reactors, 4, p.L31 - L40, 1996/00
中性子増倍率の未臨界度を推定するために、「計算誤差間接推定法」を提案する。この方法は実測値とその計算値の関連を用いて中性子増倍率の計算誤差を求めるものである。この方法をTCAで行われた中性子増倍率とパルス中性子法による実験に適用し、MCNP 4Aの計算誤差を推定した。中性子源増倍法では、測定された中性子計数率とその計算値の差から計算されたK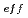 の精度を推定した。パルス中性子法では、即発中性子減衰計数の計算誤差からK
の精度を推定した。パルス中性子法では、即発中性子減衰計数の計算誤差からK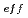 の計算誤差を求めた。
の計算誤差を求めた。
桜井 淳; 荒川 拓也*; 須崎 武則; 内藤 俶孝
JAERI-Research 95-082, 36 Pages, 1995/11
指数実験法を正方配列炉心からはずれたより複雑な配列炉心の中性子増倍率評価に適用した。精度評価をする場合、基準としては精度評価が十分になされている連続エネルギーモンテカルロ計算コードMCNP-4Aで計算した中性子増倍率の値を利用した。指数実験法で得られた精度は、従来正方配列炉心に適用していた解きに得られたものと同程度であることがわかった。
内藤 俶孝; 荒川 拓也*; 桜井 淳
JAERI-Research 95-053, 24 Pages, 1995/07
「計算誤差間接推定法」による中性子増倍率の新しい評価法を提案する。第2章には「計算誤差間接推定法」の考え方及び中性子源増倍法への適用について、第3章には原研の臨界集合体TCAの実験データを基にこの方法の妥当性の検証について記述してある。連続エネルギーモンテカルロコードMCNP-4Aで計算した中性子増倍率にこの方法を適用し、得られた結果を指数実験法で評価した中性子増倍率と比較した。その結果、両者はよく合うことがわかった。
桜井 淳; 須崎 武則; 荒川 拓也*; 内藤 俶孝
JAERI-Research 95-022, 50 Pages, 1995/03
TCAにおいて2.6%の濃縮UO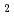 燃料棒n
燃料棒n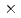 n本を正方格子間隔1.956cmで配列して、中性子源増倍法に関する実験を行った。n=17、16、14、11および8と変化させ、異なる炉心水位の組合わせで、合計15種類の未臨界炉心を構成した。
n本を正方格子間隔1.956cmで配列して、中性子源増倍法に関する実験を行った。n=17、16、14、11および8と変化させ、異なる炉心水位の組合わせで、合計15種類の未臨界炉心を構成した。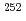 Cf中性子源を炉心中心近傍に設置し、炉心内および水反射体内の2箇所で小型核分裂計数管により垂直方向の中性子計数率分布を、5cm間隔で測定した。実験解析は、モンテカルロ法による計算コードMCNP-4Aで行った。今回つぎのような結論を得た。(1)指数実験およびMCNP-4Aで求めたk
Cf中性子源を炉心中心近傍に設置し、炉心内および水反射体内の2箇所で小型核分裂計数管により垂直方向の中性子計数率分布を、5cm間隔で測定した。実験解析は、モンテカルロ法による計算コードMCNP-4Aで行った。今回つぎのような結論を得た。(1)指数実験およびMCNP-4Aで求めたk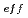 の差は、ほとんどの体系において1%以下である。(2)MCNP-4Aで50万ヒストリーで計算した中性子計数率の標準偏差は、ピーク付近でいずれも5~8%の範囲である。ひとつの炉心で規格化した中性子計数率の計算値は、実測値によく一致している。
の差は、ほとんどの体系において1%以下である。(2)MCNP-4Aで50万ヒストリーで計算した中性子計数率の標準偏差は、ピーク付近でいずれも5~8%の範囲である。ひとつの炉心で規格化した中性子計数率の計算値は、実測値によく一致している。
小林 友也*; 荒川 拓也*; 奥野 浩
JAERI-Data/Code 94-018, 36 Pages, 1994/12
連続エネルギーモンテカルロ法計算コードMCNP-4Aを評価済み核データ・ファイルJENDL-3.1と組合わせて、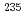 U濃縮度4.3wt%二酸化ウラン燃料棒が可溶性ガドリニウムを含む同濃縮度の硝酸ウラニル水溶液中に部分的に没している12体系の臨界実験を解析した。中性子増倍率の計算値は平均で0.955となったが、1よりこのように小さくなった主な原因は、実験報告書に記された燃料溶液等の組成の不正確さにあると推定された。このため、燃料ペレット、燃料溶液、ステンレス鋼、ガドリニウムの組成データについて吟味し、より正確な値を採用したと思われるOECD/NEAの国際ベンチマーク問題に従って解析した結果、中性子増倍率の計算値は平均で0.986となり、かなり1に近付いた。
U濃縮度4.3wt%二酸化ウラン燃料棒が可溶性ガドリニウムを含む同濃縮度の硝酸ウラニル水溶液中に部分的に没している12体系の臨界実験を解析した。中性子増倍率の計算値は平均で0.955となったが、1よりこのように小さくなった主な原因は、実験報告書に記された燃料溶液等の組成の不正確さにあると推定された。このため、燃料ペレット、燃料溶液、ステンレス鋼、ガドリニウムの組成データについて吟味し、より正確な値を採用したと思われるOECD/NEAの国際ベンチマーク問題に従って解析した結果、中性子増倍率の計算値は平均で0.986となり、かなり1に近付いた。
竹田 敏一*; 上出 英樹*; 宇根崎 博信*; 錦織 毅夫*; 佐々木 良明*; 辻本 恵一*; 荒川 恵史*; 馬野 琢也*; 鈴木 隆之*
PNC TJ265 85-01, 197 Pages, 1985/03
本報告書は次の五部から構成されている。 第一部:ZPPR-13Aの実験解析におけるマルチドロワ効果 第二部:制御棒均質化手法の改良 第三部:CADENZA追加実験解析 第四部:輸送摂動計算における差分法の改良 第五部:ZPPR-9炉心での断面積アジャストメント 第一部:ZPPR-13Aの実験解析におけるマルチドロワ効果 ZPPR-13A炉心の燃料ドロワと内部ブランケットドロワの干渉効果を取り入れる手法としてマルチドロワモデルを採用し,Keff,反応率比,反応率分布及びNaボイド反応度価値に対する補正量を計算した。 第二部:制御棒均質化手法の改良 オフセンターの制御棒の実効均質断面積をスーパーセル表面からの正味中性子流を考慮して計算する方法を導出した。この手法は,スーパーセル表面でのアルベドを用いる方法にくらべ実効均質断面積が発散する事がなく,安定した方法である。 第三部:CADENZA追加実験解析 ピンープレート炉心の核特性予測精度を調べるため,Zebra22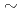 25炉心のピン,プレート体系におけるKeffのC/E値をJES3-J2断面積セットにより計算し,その違いについて検討した。第四部:輸送摂動計算における差分法の改良 輸送計算に基づく直接計算並びに輸送摂動計算より得られる反応度のくい違いについて検討した。この差はXY体系では生じないがRZ体系で生じる。この原因はXY体系では両方式の差分式が同一となるが,RZ体系では異なることに基づく。RZ体系の両方式の整合性を取るため,輸送摂動計算に付け加えるべき補正項を導出する。この補正項の大きさをNaボイド反応度に対する数値計算により検討する。 第五部:ZPPR-9炉心での断面積アジャストメント ZPPR-9炉心の核特性のC/E値を基としてJES-3-J2断面積セットより作成した16群ミクロ断面積のアジャストメントを行った。アジャストメント後の核特性のC/E値は一般によくなり,特に制御棒ワース,反応率分布のC/E値の空間依存性が下記のように少なくなった。 制御棒ワース4.1%-
25炉心のピン,プレート体系におけるKeffのC/E値をJES3-J2断面積セットにより計算し,その違いについて検討した。第四部:輸送摂動計算における差分法の改良 輸送計算に基づく直接計算並びに輸送摂動計算より得られる反応度のくい違いについて検討した。この差はXY体系では生じないがRZ体系で生じる。この原因はXY体系では両方式の差分式が同一となるが,RZ体系では異なることに基づく。RZ体系の両方式の整合性を取るため,輸送摂動計算に付け加えるべき補正項を導出する。この補正項の大きさをNaボイド反応度に対する数値計算により検討する。 第五部:ZPPR-9炉心での断面積アジャストメント ZPPR-9炉心の核特性のC/E値を基としてJES-3-J2断面積セットより作成した16群ミクロ断面積のアジャストメントを行った。アジャストメント後の核特性のC/E値は一般によくなり,特に制御棒ワース,反応率分布のC/E値の空間依存性が下記のように少なくなった。 制御棒ワース4.1%-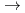 1.2% 239Pu(n,f)反応率分布3.2%-
1.2% 239Pu(n,f)反応率分布3.2%- 1.7%
1.7%