Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
徳田 伸二; 相羽 信行*
Journal of Plasma and Fusion Research SERIES, Vol.6, p.207 - 209, 2004/00
ニューコム方程式の研究の最新の進展について報告する。主として、高nキンクモードであるピーリングモードも含んだ外部モードの解析について述べる。また、低nモードについては、抵抗性壁モードの解析にも有用な理論を展開した。
徳田 伸二
Proceedings of 30th EPS Conference on Controlled Fusion and Plasma Physics (CD-ROM), 4 Pages, 2003/00
二次元Newcomb方程式に随伴する固有値問題を解くことにより、理想MHD的な摂動に対するトカマクプラズマの安定性を判定することができる。この固有値問題は、不安定なプラズマに対する成長率を与えない。しかし、成長率と固有値の間の関係を与える分散関係式を構築でき、それによって、成長率を決定することができる。分散関係式は理想MHD的な摂動に対して臨界安定に近いMHDモードの安定性を解析するための効果的な、かつ、高速な方法を提供し、かつ、臨界安定に近い場合の非理想MHDモードに対し拡張できると期待される。
徳田 伸二
プラズマ・核融合学会誌, 78(9), p.913 - 924, 2002/09
トロイダルプラズマの安定性解析の方法に関して、その最近の発展について入門的な解説を行った。臨界安定が連続スペクトルの端点になっている磁気流体力学系における摂動解析に、特に、力点をおき、そのような問題に適切な漸近接続法に注目する。そこではNewcomb方程式と内部層方程式が本質的な役割を果し、それらの数値計算法を議論する。
長家 康展; 森 貴正
Proceedings of the ANS International Topical Meeting on Advances in Reactor Physics and Mathematics and Computation into the Next Millennium (PHYSOR2000) (CD-ROM), p.13 - 0, 2000/00
複数のモンテカルロ計算の結果より原子炉パラメータの微小摂動量を求めるのは非常に困難であり、古くから相関サンプリング法、微分演算子サンプリング法等が用いられている。特に固有値問題では核分裂源分布も摂動により変化するので、核分裂源の摂動量も評価する必要があり、実効増倍率の摂動量を精度よく求めることは難しい。相関サンプリング法では中川等、北田等により核分裂源の変化による摂動量を評価する方法が提案されている。本研究では微分演算子サンプリング法における核分裂源の摂動量を評価する式を導出し、簡単な体系でその精度を検証した。その結果、相関サンプリング法、微分演算子サンプリング法とも核分裂源の変化による摂動量を考慮すると直接計算の結果とよく一致し、分散は両方法とも核分裂源の変化による摂動量の分散が支配的になるが、若干微分演算子サンプリング法の方がよいことがわかった。
徳田 伸二; 渡辺 朋子*
Physics of Plasmas, 6(8), p.3012 - 3026, 1999/08
被引用回数:58 パーセンタイル:83.31(Physics, Fluids & Plasmas)トカマクのような軸対称トロイダルプラズマにおける2次元ニューコム方程式の新しい固有値問題を提示する。この定式化においては、固有値問題のスペクトルが可算無限個の実数の固有値(点スペクトル)のみからなり、連続スペクトルを持たないように、重み関数(運動エネルギー積分)と有理面における境界条件とを設定した。理想m=1モードへ適用し、本定式化が不安定状態のみならず、安定状態も特定できること、及び、数値的に得られた固有関数が有理面で理論的に予想される特異性を示すことを実証した。
徳田 伸二; 渡辺 朋子*
統計数理研究所共同研究リポート, 110, p.70 - 77, 1998/03
トカマクプラズマ配位における2次元Newcomb方程式に随伴する固有値問題を提案する。この定式化においては重み関数(運動エネルギー積分)と有理面における境界条件を適切に選び、固有値問題のスペクトルが実可算の固有値(点スペクトル)だけから成り、連続スペクトルを持たないようにした。この定式化によって理想磁気流体力学的運動に対して、不安定状態だけでなく安定状態の特定が可能となった。
徳田 伸二; 渡邉 朋子*
JAERI-Data/Code 97-040, 105 Pages, 1997/10
トカマクのような2次元軸対象トロイダルプラズマの磁気流体力学的(MHD)安定性解析において重要な役割を果たす2次元Newcomb方程式の新しい解法を考案し、それに基づくコード(MARG2D)を開発した。新しい解法では2次元Newcomb方程式を固有値問題として解く。この際、固有関数が有利面における小さい解と正則解を正しく捉えるように重み関数(運動エネルギー積分)と有理面における境界条件を選定し、従来の困難を克服した。このコードを使うことにより、2次元配位における理想MHDモードの臨界安定状態の同定が可能になる。また、このコードは抵抗性MHD安定性解析において外部領域接続データを計算する上で不可欠である。従来の理想MHDコードERATOJとのベンチマークテストにより、MARG2Dコードで安定状態及び臨界安定状態が同定できることを実証した。
徳田 伸二; 渡辺 朋子*
プラズマ・核融合学会誌, 73(10), p.1141 - 1154, 1997/10
トカマクプラズマの抵抗性MHD安定性解析で重要な役割をはたす外部領域接続データを計算する新しい方法を提案する。この方法は、同時に、臨界安定状態を同定する理想MHD安定性解析の新しい方法でもある。この方法では、1次元の臨界安定な理想MHD状態を記述するNewcomb方程式に対する固有値問題を設定する。そして、Newcomb方程式の解の有限エネルギー部分をゼロに最も近い固有値をもつ固有関数と、その固有関数に垂直な成分に分ける。そして、垂直な成分の満たすべき特異方程式を導く。また、積分関数式を適用して有限エネルギー部分から接続データを計算する。接続データを解析的に求めることのできるm=1モード(m:ポロイダルモード数)に本方法を適用し、その有効性を実証した。
植木 太郎*; 森 貴正; 中川 正幸
Nuclear Science and Engineering, 125(1), p.1 - 11, 1997/00
モンテカルロ法による固有値(実効増倍率)計算における、分散及びサイクル間の共分散の評価法に対する理論的検討を行った。その結果、真の分散及び共分散と、通常のモンテカルロ計算で評価されている見かけの分散及び共分散との関係式が得られた。この関係式に基づいて、通常のモンテカルロ計算の結果から反復法による真の分散(分散のバイアス)の評価法を考案した。いくつかの問題に本評価法を適用した結果、真の分散と見かけ分散の比が1.4から3.1の問題に対しては極めて有効であることが明らかになった。さらに、分散の比が5以上となる問題においても、本評価法によって70%以上の確率で真の値の40%以内で標準偏差(分散の平方根、計算結果の統計誤差)を評価することが可能であった。
徳田 伸二; 渡邉 朋子*
JAERI-Data/Code 95-011, 71 Pages, 1995/08
1次元Newcomb方程式の外部領域接続データを数値的に求めるMARG1Dコードを開発した。接続データはトカマク・プラズマの抵抗性MHD安定性解析で重要な役割をはたす。MARG1Dコードでは接続データを境界値問題法および固有値問題法によって接続データを求める。解くべき問題に対応する変分原理を導き、有限要素法を適用する。臨界安定な場合を除けば、境界値問題法と固有値問題法は同等である。しかし、固有値問題法はいくつかの利点を持っている。すなわち、この方法は臨界安定な状態を同定できる理想MHD安定性解析の新しい方法である。また、臨界安定に近い場合の接続データを計算するにあたって数値的安定性を保証する。数値実験によってMARG1Dコードは高精度な接続データを与えることを示す。
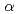 -and
-and  -manganese
-manganese佐々木 健; 別役 広; 森 信郎*; 鵜飼 武*
Journal of Magnetism and Magnetic Materials, 31-34, p.41 - 42, 1983/00
被引用回数:4 パーセンタイル:35.50(Materials Science, Multidisciplinary)ハーバード型のハミルトニアンを用いて強く束縛された近似のバンド計算を行ない、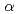 マンガンの対称単位胞中の29原子の磁気モーメントと方向を自己無接着に決定した。採用したエネルギー積分は、KKR法で計算した
マンガンの対称単位胞中の29原子の磁気モーメントと方向を自己無接着に決定した。採用したエネルギー積分は、KKR法で計算した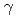 マンガンのバンド構造から決定した。固有値解法プログラムは高度にベクトル化されていて、580
マンガンのバンド構造から決定した。固有値解法プログラムは高度にベクトル化されていて、580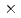 580次元のハミルトニアンに対して、7倍の加速因子がえられた。同様の方法で
580次元のハミルトニアンに対して、7倍の加速因子がえられた。同様の方法で マンガンの可能な時期構造について研究を行なった。これらの問題は、再起連分数法によっても、異なる視点から考察された。
マンガンの可能な時期構造について研究を行なった。これらの問題は、再起連分数法によっても、異なる視点から考察された。
藤村 統一郎; 筒井 恒夫
JAERI-M 8253, 133 Pages, 1979/05
固有値問題を解く数値解法のアルゴリズムの調査(JAERI-memo6225)に引き続いて、それらに基づいた解法プログラムが開発・整備され、既存のプログラムとの比較がなされた。EISPACK-Jは米国ANLの固有値問題専用パッケージEISPACK-2を発展させたものであり、複素行列の標準問題や実行例の一般問題を解くほか、必要な固有値や固有ベクトルのみを求める特殊問題も解くことができる。また、変った機能をもつ8件のプログラムも整備されたが、これらはベンチマーク・テストを通して、その特徴が明らかにされる。テストには実験規模の問題を含む多くの問題が用意され、各プログラムの計算に要する計億領域、計算時間、解の精度について検討された。その結果、Householder法、QR法、それに逆反復法に基づくEISPACK-Jのプログラムは計算時間および精度について優れていることが示された。
西田 雄彦; 堀上 邦彦; 鈴木 忠和; 中原 康明; 田次 邑吉; 朝岡 卓見
JAERI-M 6251, 36 Pages, 1975/09
原子炉系の固有値計算を行う場合の加速法の一つとして、汎用モンテカルロ輸送コード「MORSE」に粗メッシュ再鈎合い法を適用した。ここでは、モンテカルロ・ゲームから得られる情報の内、必要な量だけを集積・処理するルーチン「COARSE」と、これに引続いて再鈎合い係数を計算するルーチン「REBAL」を作成し、、「MORSE」を拡張した。これらのルーチンの詳細と共に、モンテカルロ法における粗メッシュ再鈎合い加速法のアルゴリズムについて報告する。