Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
J-N.G.Leboeuf*; 栗田 源一
JAERI-Research 98-010, 15 Pages, 1998/03
JAERI-Research-98-010.pdf:0.76MB
米国オーク・リッジ国立研究所で開発されたトロイダルMHDコードFARと日本原子力研究所で開発されたAEOLUSコードを使って、注意深く作られたベンチマーク用の分布とパラメータの平衡に対して計算された線形の抵抗性MHD安定性の結果を比較した。これらの分布は、トロイダル・モード数n=1のチアリング・モードに対して不安定な分布である。双方のコードによって計算された固有値と固有関数は、非常に良く一致し、これらのモードに対して圧縮性の効果は弱いことが示された。FARコードとAEOLUSコードで計算された有限のプラズマ圧力の場合のテアリング・モードの成長率も良い一致を示した。有限ベータは、トロイダル・テアリング・モードに対して安定化の効果を持つこと、また圧縮性の効果は、有限ベータのテアリング・モードに対しても弱いことが示された。
藤村 薫
原子力工業, 41(3), p.49 - 51, 1995/00
流体系における層流から乱流への遷移の素過程としての、流体運動の安定性と分岐について述べ、代表的な例として、現在行っている縦横モード相互作用に関する研究の解説を行った。不安定成層をしたせん断流においては、ベナール対流に対応するロールが流れ方向に軸をもって現われる。しかし、せん断流を強くしてゆくと、流体力学的不安定モードである流れ方向に周期性をもつ伝播波が現われる。縦ロールと横伝播波が同時に出現するパラメータ領域ではどのような空間パターンが形成されうるかについて、弱非線形理論に基づく結果を紹介し、展望について述べた。
藤村 薫; 水島 二郎*
日本物理学会誌, 47(10), p.798 - 805, 1992/10
流体運動における解の分岐現象は、力学系理論の進展によって近年脚光を浴びている。分岐現象の解析においては、無限自由度系である流体方程式から有限小数自由度系である「振幅方程式」への自由度の低減が不可欠である。本解説では、この自由度の低減を中心課題として発展してきた流れの弱非線形安定性理論を解説する。とりわけ、簡単な対称群との可換性の要請の下に得られる振幅方程式の分類、中心多様体定理に基づく振幅方程式の導出、並びに振幅方程式によって記述される解のダイナミックスについて述べる。
水島 二郎*; 藤村 薫
J. Fluid Mech., 234, p.651 - 667, 1992/00
被引用回数：21 パーセンタイル：68.03(Mechanics)ベナール対流中の2次元準中立攪乱間に波数比1:3の高調波共鳴が生じることを明らかにした。共鳴が生じる場合、共鳴モードの振幅に対する方程式を導き、分岐パラメータとしてレイリー数をとった際の分岐特性を調べた。その結果、低プラントル数流に対しては伝播波解とその変調波解が安定に存在しうる領域のあることが明らかになった。なお、臨界モードが別個に存在する場合の相互作用を評価し、高波数域以外では1:3共鳴の結果得られた解は臨界モードに対し不安定であることが結論された。
藤村 薫
Philos. Trans. R. Soc. Lond., Ser. A, 340, p.95 - 130, 1992/00
2枚の異なる温度を有する鉛直平板間に満たされた流体層には温度差が十分小さくても自然対流が生じる。温度差を大きくしていくと、自然対流にロール対流又は波動が重畳されてくる。本研究では適当な波数とグラスホフ数を選んだ場合、ロール対流同士の非線形高調波共鳴、ロールと波動間の共鳴、ロール同士と波動間の共鳴という異なる3種の共鳴が生じることを指摘し、各々の場合について各モードの振幅を記述する方程式を導き、振幅方程式の解の分岐特性を調べた。
水島 二郎*; 藤村 薫
European Journal of Mechanics B, Fluids, 10(2(SUPPL.)), 331 Pages, 1991/00
固体-固体境界条件下におけるBenard対流に生じる2次元ロール解の平衡状態を調べた。波数比1:3の高調波共鳴が生じることを指摘した。その際、可能な分岐解として高プラントル数ではpureモードとmixedモードが存在し、低プラントル数では伝播波モード、安定な変調伝播波モード、pureモード、及びmixedモードが存在することが明らかになった。
藤村 薫; 水島 二郎*
European Journal of Mechanics B, Fluids, 10(2(SUPPL.)), p.25 - 30, 1991/00
異なる一様温度を有する鉛直平板間に満たされた自然対流の非線形安定性を弱非線形漸近理論に基づいて調べた。撹乱振幅の時間発展を記述する方程式として、プラントル数PがP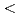
Pc(Pc=12.45425644)のときLandau方程式が、P
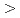Pcのとき2-連立Landau方程式が、P=Pcのとき3-連立Landau方程式が導かれた。方程式に含まれる係数を数値的に決定し、振幅方程式の平衡解をいくつかのカテゴリーに分類し、平衡解の線形安定性を議論した。
藤村 薫
Phys. Fluids A, 2(7), p.1182 - 1190, 1990/07
被引用回数：0 パーセンタイル：0.00(Mechanics)円管内面に沿って回転する液膜流の安全性を線形理論を用いて調べた。ただし、円管は静止しているものとし、円管内での回転は仮想的な円周方向の外力によって維持されると仮定している。この流れの不安定モードとしては、傾斜平板上を流れ落ちる液膜流に固有の液膜モードと、遠心力不安定モードが得られる。これに対し、管軸方向に新たな外力を付加することにより、軸方向のせん断流が、遠心力不安定モードを安定化することが示された。
藤村 薫
Phys.Fluids A, 30(4), p.1216 - 1218, 1987/04
高温伝熱機器の流体振動の発生原因に挙げられる流れの不安定波の挙動を解析する際、Landau定数を求めることが必要となる。Landau定数には2通りの定義があり、両者の相違点についてこれまで大まかな議論しかされていなかった。ここでは平行平板間を流れるポワズイユ流を対称に両者の差異を定量的におさえた。
藤村 薫; 水島 二郎*; 後藤 金英*
ながれ, 4(3), p.213 - 223, 1985/00
高温伝熱機器における流体振動の問題や、上鏡部自然対流の問題などでは、冷却材の安定性、とりわけ、有限振幅の速度変動の挙動を把握することが重要である。ここでは、二次元平行流に対する非線形安定性理論のレビューを行い、問題点を指摘し、更に、一つの新しい解決策についての解説を行う。
藤村 薫
JAERI-M 9212, 16 Pages, 1980/11
2次元Poiseuille流に対する助走区間における入口流れの線形安定性を調べた。速度分布はSpparow,Lin&Lundgrenによる結果を用いた。この研究はChen;Chen&Spparowの追試に相当する。今回の計算の目的は2次元入口流れに関する中立安定撹乱の臨界位相温度に、2次元せん断乱流や収束するタイプのJeffery-Hamel流にみられるような漸近値が存在するか否かについての知見を得ることにある。計算は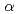
R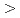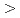1のときのOrr-Sommerfeld方程式の漸近解を用いた方法で行った。その結果、2次元入口流れの場合上記のような臨界位相速度の漸近値は存在せず、入口流れのパラメーターX
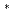の減少に伴なって、完全に発達した2次元Poiseuille流の臨界位相速度Cc=0.2668から単調に増加することが明らかになった。
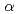R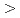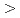1, 1位の転移点を1つ有するOrr-Sommerfeld方程式の固有値問題の漸近解を用いた解法-2次元準平行流-Jeffery-Hamel流に対する計算コード藤村 薫
JAERI-M 9164, 72 Pages, 1980/11
流れの内在的安定性の線形理論における基礎方程式であるOrr-Sommerfeld方程式の固有値問題を、漸近解を用いた方法で解く計算コードを作成した。このコードは撹乱の波数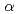とReynolds数Rの積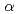R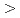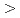1での、1位の転移点を1つ有する場合の速度場に適用することができ、ここではそういった流れの代表例として2次元Poiseuille流をも含むJeffery-Hamel流に対する計算コードについて詳述する。このコードは上記の様な種々の流れ場に直ちに拡張しうるものである。
