Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
長谷川 雄太; 小野寺 直幸; 朝比 祐一; 伊奈 拓也; 今村 俊幸*; 井戸村 泰宏
Fluid Dynamics Research, 55(6), p.065501_1 - 065501_25, 2023/11
被引用回数：1 パーセンタイル：0.00(Mechanics)格子ボルツマン法(LBM)に基づくラージエディーシミュレーション(LES)に対するデータ同化の適用性を調査した。2次元等方乱流の観測システムシミュレーション実験を行い、空間的に疎かつノイズを含む観測を用いてナッジング法及び局所アンサンブル変換カルマンフィルタによるデータ同化の精度を検証した。LETKFの利点として、ナッジングで必要となる空間補間及び巨視的量(流体密度及び流速)からLBMの速度分布関数への変換を必要としないことが挙げられる。計算条件として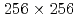
格子及び10%の流速観測ノイズを設定した実験では、64アンサンブルのLETKFは
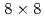の観測点(計算格子点数に対して0.1%程度)でも観測ノイズよりも小さい誤差を示した。これは、ナッジングで同様の精度を示すのに1桁程度多くの観測点数を要する精度である。さらに、LETKFでは観測点数の不足はエネルギースペクトルの振幅には影響せず、スペクトルの位相誤差のみに影響することが確認された。以上の結果により、LETKFは、空間的に疎かつノイズを含む観測を用いた2次元のLBM計算のデータ同化に対してロバストかつ高精度であることが示された。
伊奈 拓也; 井戸村 泰宏; 今村 俊幸*; 小野寺 直幸
Proceedings of International Conference on High Performance Computing in Asia-Pacific Region (HPC Asia 2023) (Internet), p.29 - 34, 2023/02
ヤコビ前処理による混合精度クリロフソルバは、ヤコビ前処理をFP16やBF16のような低精度で計算した場合しばしば著しい収束性の悪化を示すことがある。この収束性の悪化はデータ変換時の丸め誤差により対角優位性が失われることに起因することがわかった。この問題を解決するために、元の行列データの対角優位性を保つように設計された新しいデータ変換方法を提案する。NVIDIA V100 GPU上でポアソン方程式を共役勾配法、双共役勾配安定化法、一般化最小残差法にFP16/BF16ヤコビ前処理を組み合わせた混合精度クリロフソルバによって計算することによって提案手法を検証する。データ変換はCUDAの組み込み関数を利用して最近接丸め、正の無限大丸め、負の無限大丸め、ゼロ方向丸めを切り替えて実装し、これが主反復の前に一度だけ呼び出される。したがって、提案するデータ変換にかかるコストは無視できる程度に小さい。連立一次方程式をスケーリングして行列の係数を連続的に変化させた場合に、最近接丸めによる従来のデータ変換では、対角係数と非対角係数の丸め誤差に依存して収束性が周期的に変化する。ここで、収束性悪化の周期と大きさは仮数部のビット長に依存する。一方、提案するデータ変換方式では収束性悪化を完全に回避できることが示され、ヤコビ前処理において余分なコストを伴わないロバストな混合精度計算が可能となった。
長谷川 雄太; 今村 俊幸*; 伊奈 拓也; 小野寺 直幸; 朝比 祐一; 井戸村 泰宏
Proceedings of 13th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Heterogeneous Systems (ScalAH22) (Internet), p.10 - 17, 2022/00
格子ボルツマン法(LBM)に基づく数値流体力学シミュレーションおよび局所アンサンブル変換カルマンフィルタ(LETKF)によるアンサンブルデータ同化をNVIDIA A100 GPU搭載スパコンに対して実装し、および最適化した。LBMとLETKFの協働のため、データ転置通信を実装し、LETKFのデータ依存性に基づいて計算,ファイルI/O、および通信のオーバーラップにより通信を最適化した。2次元等方乱流,アンサンブル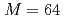数
,格子点数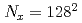
の条件において、通信を最適化した実装は、LETKFを並列化しない単純な実装に対して3.85倍の高速化を達成した。LETKFの主要な計算カーネルは
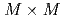の実対称密行列の固有値分解であり、その計算のため、バッチ形式固有値分解ソルバEigenGを新たに開発した。EigenGによるバッチ形式固有値分解は、既存ライブラリであるcuSolverに対して64倍の高速化を達成した。
山田 進; 今村 俊幸*; 町田 昌彦
Supercomputing Frontiers, p.1 - 19, 2022/00
被引用回数：0 パーセンタイル：0.00(Computer Science, Theory & Methods)本発表は科学研究費補助金(科研費)研究「エクサスケール計算機を想定した量子モデルシミュレーションに対する並列化・高速化」の一環として実施した量子問題計算に現れる大規模な対称疎行列の複数固有値を求める計算をGPUを用いて高速に計算する方法についての報告である。GPU側のメモリは小さいため、大規模な問題をGPUを用いて計算するとき、すべてのデータをGPU側のメモリに格納することができず、一部のデータをCPU側のメモリに格納することになるが、CPUとGPU間のデータのやり取りには多くの時間がかかる。そこで、LOBPCG法のアルゴリズムの特徴を考慮してこのデータのやり取りを削減する方法を提案した。実際に原子力機構のスパコンHPE SGI8600のGPUシステムを用いた並列計算から提案方法を用いることで高速化を実現できることを確認した。この成果は、固有値計算の高速計算だけでなく、現在の主流の1つであるGPU計算機の有効利用に資する成果でもある。
伊奈 拓也*; 井戸村 泰宏; 今村 俊幸*; 山下 晋; 小野寺 直幸
Proceedings of 12th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems ScalA21) (Internet), 8 Pages, 2021/11
被引用回数：2 パーセンタイル：41.91(Computer Science, Software Engineering)多相熱流動解析コードJUPITERにおける前処理付き共役勾配法(P-CG)ソルバおよびマルチグリッド前処理付き共役勾配法(MGCG)ソルバに対して反復改良(IR)法に基づく新しい混合精度前処理を開発した。このIR前処理では全てのデータを半精度で格納してメモリアクセスを削減するが、全ての演算処理を単精度で行う。このハイブリッド半精度/単精度実装は単精度処理と同様の収束特性を維持しつつ、計算性能は半精度処理に近くなる。開発ソルバを富岳(A64FX)で最適化し、JUPITERの悪条件行列に適用した。新しいIR前処理を用いたP-CGソルバとMGCGソルバは8,000ノードまで良好な強スケーリングを示し、8,000ノードにおいて、これらのソルバはOakforest-PACS(KNL)における従来ソルバに比べてそれぞれ4.86倍および2.39倍に高速化された。
井戸村 泰宏; 伊奈 拓也*; Ali, Y.*; 今村 俊幸*
第34回数値流体力学シンポジウム講演論文集(インターネット), 6 Pages, 2020/12
ジャイロ運動論的トロイダル5次元full-fオイラーコードGT5Dにおける半陰解法差分計算用に新しいFP16(半精度)前処理付き省通信クリロフソルバを開発した。このソルバでは、大域的集団通信のボトルネックを省通信クリロフ部分空間法によって解決し、さらに収束特性を向上するFP16前処理によって袖通信を削減した。FP16前処理は演算子の物理特性に基づいて設計し、A64FXで新たにサポートされたFP16SIMD処理を用いた実装した。このソルバをGPUにも移植し、約1,000億格子のITER規模計算の性能を富岳(A64FX)とSummit(V100)で測定した。従来の非省通信型ソルバに比べて、新しいソルバはGT5Dを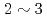
倍加速し、富岳とSummitの両方で5,760CPU/GPUまで良好な強スケーリングが得られた。
井戸村 泰宏; 伊奈 拓也*; Ali, Y.*; 今村 俊幸*
Proceedings of International Conference for High Performance Computing, Networking, Storage, and Analysis (SC 2020) (Internet), p.1318 - 1330, 2020/11
被引用回数：2 パーセンタイル：34.38(Computer Science, Information Systems)5次元ジャイロ運動論モデルに基づく次世代核融合実験炉ITERのマルチスケールfull-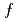
シミュレーションは核融合科学において最も計算コストが大きい問題の一つである。本研究では、新しい混合精度省通信クリロフ法を用いてジャイロ運動論的トロイダル5次元オイラーコードGT5Dを高速化した。演算加速環境における大域的集団通信のボトルネックを省通信クリロフ法によって解決した。これに加えて、A64FXにおいて新たにサポートされたFP16SIMD演算を用いて設計された新しいFP16前処理により、反復(袖通信)の回数と計算コストの両方を削減した。富岳とSummitにおける1,440CPU/GPUを用いた1,000億格子のITER規模シミュレーションに対して、提案手法の処理性能は従来の非省通信クリロフ法に比べてそれぞれ2.8倍, 1.9倍高速化され、5,760CPU/GPUまで良好な強スケーリングを示した。
井戸村 泰宏; 伊奈 拓也*; Ali, Y.*; 今村 俊幸*
Proceedings of Joint International Conference on Supercomputing in Nuclear Applications + Monte Carlo 2020 (SNA + MC 2020), p.225 - 230, 2020/10
ジャイロ運動論的トロイダル5次元オイラーコードGT5Dにおける半陰解法差分ソルバ向けに新しいFP16(半精度)前処理付き省通信型クリロフソルバを開発した。このソルバでは、大域的集団通信のボトルネックを省通信型クリロフ部分空間法を用いて解決し、FP16前処理を用いて収束特性を改善することで袖通信の回数を削減した。FP16前処理は演算子の物理特性に基づいて設計され、A64FXにおいて新たにサポートされたFP16SIMD演算を用いて実装された。本ソルバは富岳(A64FX)とSummit(V100)に移植され、JAEA-ICEX(Haswell)に比べてそれぞれ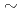
63倍, 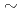29倍のソケットあたり性能の向上を達成した。
井戸村 泰宏; 小野寺 直幸; 山田 進; 山下 晋; 伊奈 拓也*; 今村 俊幸*
スーパーコンピューティングニュース, 22(5), p.18 - 29, 2020/09
多相多成分熱流動解析コードJUPITERの圧力ポアソン方程式に省通信型マルチグリッド前処理付き共役勾配(CAMGCG)法を適用し、従来のクリロフ部分空間法と計算性能と収束特性を比較した。CAMGCGソルバは問題サイズによらずロバーストな収束特性を示し、通信削減と収束特性向上を両立することから、通信削減のみを実現する省通信クリロフ部分空間法に対する優位性が高い。CAMGCGソルバを900億自由度の大規模多相流体解析に適用し、前処理付共役勾配法ソルバと処理性能を比較した。このベンチマークにおいて、反復回数は約1/800に削減され、Oakforest-PACS上で8,000ノードに至る良好な強スケーリングを維持しつつ約11.6倍の性能向上を達成した。
山田 進; 町田 昌彦; 今村 俊幸*
Parallel Computing; Technology Trends, p.105 - 113, 2020/00
被引用回数：1 パーセンタイル：32.67(Computer Science, Hardware & Architecture)本発表は科学研究費補助金(科研費)に従い実施した強相関ハバードモデル計算に現れる固有値問題に対する高性能計算に関するものである。具体的には、ハバードモデルの計算に現れる固有値計算に固有値計算ソルバの1つであるLOBPCG法を適用した際の高速化についての発表である。特筆すべき成果は、現在主流のプロセッサの1つであるGPUのアーキテクチャに合わせたデータの格納方法を提案し、実際に行列計算を高速化したことである。さらに、複数の線形計算をまとめて実行することで、データへのアクセス回数を減らすことができ、さらなる高速化も実現した。これらの高速化により、これまでの方法と比較し全体で約1.4倍の高速化を実現した。なお、この成果は科研費研究「エクサスケール計算機を想定した量子モデルシミュレーションに対する並列化・高速化」の研究成果である一方、GPUを利用した高性能計算にも資する成果である。
Ali, Y.*; 小野寺 直幸; 井戸村 泰宏; 伊奈 拓也*; 今村 俊幸*
Proceedings of 10th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA 2019), p.1 - 8, 2019/11
被引用回数：11 パーセンタイル：95.86(Computer Science, Theory & Methods)大規模線形問題の反復法ソルバはCFDコードで共通に用いられる。前処理付共役勾配(P-CG)法は最も広く用いられている反復法の一つである。しかしながら、P-CG法では、特に演算加速環境において、大域的集団通信が重要なボトルネックとなる。この問題を解決するために、省通信版のP-CG法がますます重要になっている。本論文では多相CFDコードJUPITERにおけるP-CG法と前処理付チェビシェフ基底省通信CG(P-CBCG)法を最新のV100GPUに移植する。全てのGPUカーネルは高度に最適化され約90%のルーフライン性能を達成し、ブロックヤコビ前処理はGPUの高い演算性能を引き出すように再設計し、さらに残された袖通信のボトルネックは通信と計算のオーバーラップによって回避した。P-CG法とP-CBCG法の全体性能は大域的集団通信と袖通信の省通信特性によって左右され、GPUあたりのノード間通信帯域が重要となることが示された。開発したGPUソルバはKNLにおける以前のCPUソルバの2倍に加速され、Summitにおいて7,680GPUまで良好な強スケーリングを達成した。
井戸村 泰宏; 伊奈 拓也*; 山下 晋; 小野寺 直幸; 山田 進; 今村 俊幸*
Proceedings of 9th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA 2018) (Internet), p.17 - 24, 2018/11
被引用回数：8 パーセンタイル：92.04(Computer Science, Theory & Methods)多相流体CFDコードJUPITERの圧力ポアソン方程式に省通信マルチグリッド前処理付共役勾配(CAMGCG)法を適用し、省通信クリロフ部分空間法と計算性能と収束特性を比較した。JUPITERコードにおいてCAMGCGソルバ問題サイズによらずロバーストな収束特性を有し、通信削減と収束特性向上を両立することから、通信削減のみを実現する省通信クリロフ部分空間法に対する優位性が高い。CAMGCGソルバを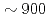
億自由度の大規模多相流体CFDシミュレーションに適用して反復回数を前処理付CG法の
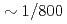に削減し、Oakforest-PACSにおける8,000ノードまでの良好な強スケーリングとCG法の
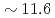倍の性能向上を達成した。
山田 進; 今村 俊幸*; 町田 昌彦
Lecture Notes in Computer Science 10776, p.243 - 256, 2018/00
被引用回数：1 パーセンタイル：32.84(Computer Science, Artificial Intelligence)本発表は科学研究費補助金(科研費)研究の一環として実施した量子問題計算に現れる大規模な対称疎行列であるハミルトニアン行列の複数の固有値および固有ベクトルを計算する際に用いる省通信ノイマン展開前処理の有効性についての報告である。具体的な成果は、ハミルトニアン行列の複数の固有値とそれに対応する固有ベクトルをLOBPCG法を用いて反復計算する際の収束性を向上させるための新規の前処理方法を提案し、実際の計算から既存の方法よりも短時間で計算できることを示したことである。さらに、問題の物理的性質を利用して前処理計算の通信回数を減少させるアルゴリズムを提案し、原子力機構のスパコンSGI ICEXおよび理化学研究所の京スパコンの数千コアを用いた並列計算において、高速化が実現することを確認した。この成果は、量子計算の高速計算だけでなく、今後大規模化していく並列計算機の有効利用に資する成果でもある。
井戸村 泰宏; 伊奈 拓也*; 真弓 明恵; 山田 進; 今村 俊幸*
Lecture Notes in Computer Science 10776, p.257 - 273, 2018/00
被引用回数：2 パーセンタイル：48.24(Computer Science, Artificial Intelligence)前処理付チェビシェフ基底省通信共役勾配(P-CBCG)法を多相熱流体CFDコードJUPITERにおける圧力ポアソン方程式に適用し、8,208台のKNLプロセッサを搭載したOakforest-PACS上で計算性能と収束特性を前処理付共役勾配(P-CG)法や前処理付省通信共役勾配(P-CACG)法と比較した。P-CBCG法は収束特性のロバースト性を維持しつつ集団通信回数を削減する。このロバースト性向上により、P-CACG法と比べて一桁以上大きい省通信ステップ数を実現する。2,000プロセッサを用いた場合、P-CBCG法はP-CG法, P-CACG法と比べてそれぞれ1.38倍, 1.17倍高速であることを示した。
山田 進; 今村 俊幸*; 町田 昌彦
Parallel Computing is Everywhere, p.27 - 36, 2018/00
本発表は科研費研究の一環として実施した固有値計算ソルバLOBPCG法の前処理に関する研究についての発表である。LOBPCG法は反復解法であり適切な前処理を用いることで収束性が向上することが知られているが、量子問題に表れるハバードモデルの固有値を計算する際に物理パラメータによっては既存の前処理では収束性が向上しないことがある。そこで、線形方程式の反復解法で前処理として使われているノイマン展開を利用した前処理を適用し、そのような問題に対しても収束性が向上することを見出した。さらに、問題の物理的性質を考慮し、演算回数は若干増加するが、通信回数を減少させる方法を提案した。この方法で開発したコードを、原子力機構の並列計算機SGI ICEXを用いて並列シミュレーションしたところ、これまでの方法よりも約20%高速に計算できることを確認した。この成果は、固有値問題に有効な前処理方法を見出しただけではなく、ネットワーク構造が複雑化してきている並列計算機での性能向上にも資する成果である。
井戸村 泰宏; 伊奈 拓也*; 真弓 明恵; 山田 進; 松本 和也*; 朝比 祐一*; 今村 俊幸*
Proceedings of 8th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA 2017), p.7_1 - 7_8, 2017/11
ジャイロ運動論的5次元オイラーコードGT5Dに省通信一般化最小残差(CA-GMRES)法を適用し、一般化共役残差(GCR)法を用いたオリジナルコードとの性能比較をJAEA ICEX(Haswell)、Plasma Simulator(FX100)、Oakforest-PACS(KNL)において実施した。CA-GMRES法はGCR法に比べて約3.8倍の演算密度となることから、メモリとネットワークの帯域が制限された将来のエクサスケールアーキテクチャに適合する。性能評価の結果、GCR法に比べて計算カーネルは1.47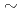2.39倍加速され、1,280ノード処理におけるデータ縮約通信は全体コストの5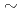13%から約1%に削減された。
山田 進; 伊奈 拓也*; 佐々 成正; 井戸村 泰宏; 町田 昌彦; 今村 俊幸*
Proceedings of 2017 IEEE International Parallel & Distributed Processing Symposium Workshops (IPDPSW) (Internet), p.1418 - 1425, 2017/08
被引用回数：3 パーセンタイル：57.86(Computer Science, Hardware & Architecture)本発表では、BaileyのDouble-Doubleアルゴリズムを利用した4倍精度基本線形代数演算ライブラリ「BLAS」の高速化と、それを4倍精度固有値計算ルーチンに適用した際の計算性能の向上について発表する。特筆すべき成果は、積和演算の中間結果を高精度で保持して計算できるFMA命令を利用することで、我々がこれまでに開発した4倍精度BLASと比較し、代表的なルーチンで20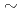45%の高速化を実現したことである。さらに、4倍精度固有値ソルバ「QPEigenK」が利用している4倍精度BLASをFMA命令を利用して開発したものに置き換えるだけで、原子力機構のICE Xおよび東京大学のFX10の2つのスパコンの大規模並列計算において10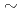20%の高速化を実現した。この成果は、計算機の大規模化に伴って必要になりつつある高精度計算の高速な実行に資する成果である。
真弓 明恵; 井戸村 泰宏; 伊奈 拓也; 山田 進; 今村 俊幸*
Proceedings of 7th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA 2016) (Internet), p.17 - 24, 2016/11
左前処理省通信共役勾配(LP-CA-CG)法を多相数値流体力学コードJUPITERの圧力Poisson方程式に適用した。LP-CA-CG法の演算密度を分析し、内積処理と三項間漸化式処理のループ分割を行うことで演算密度を大きく向上した。ブロックヤコビ前処理及びアンダーラップ前処理を適用した2つのLP-CA-CGソルバを開発した。京コンピュータ上では局所的な1対1通信のスケールが良好であることと、アンダーラップ前処理を適用すると収束性が悪くなることにより、ブロックヤコビ前処理ソルバにより良好な性能が得られた。このソルバは3万ノードまで良好な強スケーリングを示し、大域的集団通信のコストを69%削減することにより従来のCG法ソルバに比べて高い性能を達成した。
佐々 成正; 山田 進; 町田 昌彦; 今村 俊幸*
Nonlinear Theory and Its Applications, IEICE (Internet), 7(3), p.354 - 361, 2016/07
フールエ変換を連続使用した場合の丸め誤差の累積誤差について議論を行った。偏微分方程式の数値計算において、フールエ変換を繰り返し連続使用した場合に丸め誤差が累積することを確認した。計算精度の毀損を補うため4倍精度高速フーリエ変換を用いた計算を行って有効性を確認した。
山田 進; 今村 俊幸*; 町田 昌彦
Parallel Computing; On the Road to Exascale, p.361 - 369, 2016/00
被引用回数：1 パーセンタイル：41.84(Computer Science, Hardware & Architecture)本発表では簡単な演算を高速に実行できるアクセラレータ(補助演算装置)の1つであるGPUを用いてハバードモデルの計算に現れる固有値問題を高速に計算する手法について発表する。特筆すべき成果は、ハバードモデルの物理的性質、およびGPUの構造を考慮してデータの格納形式や計算方法を考案したところ、GPUで一般的に利用されている計算方法よりも約2倍高速に計算できることを実際のGPUを利用した計算から示したことである。さらに、6コアのCPUを用いた並列計算と比較しても、23倍高速に計算できることを確認した。この成果は、今後高性能計算において主流になると考えられているアクセラレータを利用した計算機の有効利用に資する成果である。
