Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
山本 俊弘; 桜井 淳; 内藤 俶孝*
Annals of Nuclear Energy, 25(9), p.599 - 607, 1998/00
被引用回数：1 パーセンタイル：14.67(Nuclear Science & Technology)従来の中性子源増倍法による未臨界度測定法の欠点を補うために、「計算誤差間接推定法」を提唱した。この手法は、計算で求めた実効増倍率のバイアスを、中性子計数率の測定値と計算値との差から求めるものである。このバイアスを、計算で求めた実効増倍率の補正に使うことにより、より真値に近い実効増倍率を導くことができる。この手法の検証を行うために、中性子源増倍法を模擬した数値実験を中性子拡散計算で行った。この手法によって真の実効増倍率がどの程度再現できるかが示された。その結果、この手法によって未臨界度を高精度に評価するためには、少なくとも三ヵ所での中性子反応率の測定が必要であることが分かった。
桜井 淳; 山本 俊弘; 荒川 拓也*; 内藤 俶孝*
日本原子力学会誌, 40(5), p.380 - 386, 1998/00
被引用回数：0 パーセンタイル：0.00(Nuclear Science & Technology)TCAで実施された二分割結合炉心実験の解析をMCNP 4Aで行った。中性子増倍率の誤差は、筆者らによって提案された「計算誤差間接推定法」で評価した。パルス中性子法シミュレーション計算は17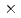
17+5G+17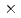17体系に対して、指数実験法シミュレーションの計算は16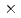9+3G+16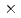9体系及び16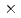9+5G+16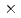9体系に対して行った。「計算誤差間接推定法」による評価によれば、MCNP 4Aで計算した中性子増倍率には、0.4~0.9%の誤差が見込まれる。従来のパルス中性子法及び指数実験法では中性子増倍率に6%の誤差が見込まれているが、「計算誤差間接推定法」による計算値を用いた未臨界度の評価ではそれを1%以下にできる。
桜井 淳; 山本 俊弘; 荒川 拓也*; 内藤 俶孝
Journal of Nuclear Science and Technology, 34(6), p.544 - 550, 1997/06
被引用回数：2 パーセンタイル：22.76(Nuclear Science & Technology)転水減速・反射、低濃縮UO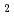
燃料格子炉心での未臨界実験に「計算誤差間接推定法」を適用して未臨界度を推定した。即発中性子減衰定数と空間減衰定数の二つの測定可能な量をMCNP 4AとJENDL-3.2を用いて計算し、その誤差から「計算誤差間接推定法」により反応度とのバイアスを求めた。空間減衰定数の計算値と測定値との差は、実験値の誤差とほぼ同等であった。これにより、MCNP 4AおよびJENDL-3.2を用いた未臨界推定精度は、指数実験で達成可能な精度の範囲内であると言える。一方、計算および測定で求めた即発中性子減衰定数の差から、計算で求めた反応度のバイアスは有意な値が得られた。このバイアス値より計算で求めた実効増倍率に対して補正を行い、未臨界度を推定した。
山本 俊弘; 桜井 淳; 荒川 拓也*; 内藤 俶孝
Journal of Nuclear Science and Technology, 34(5), p.454 - 460, 1997/05
被引用回数：5 パーセンタイル：42.30(Nuclear Science & Technology)体系の未臨界度を推定するために、「計算誤差間接推定法」という新しい手法を提案する。直接測定の出来ない実効増倍率の「測定値」とその計算値とを比べるのではなく、未臨界実験で測定可能な量の測定値と計算値とを直接比べることで実効増倍率の計算値のバイアスを見積もる。未臨界計算の精度は、これらの測定可能な量の誤差から間接的に導かれる。ここでは、中性子源増倍法、パルス中性子法、指数実験法に基づく三つの推定法を示す。この三つの手法について、それぞれ中性子計数率分布、即発中性子減衰定数、空間減衰定数が計算と推定で比較され、実効増倍率の計算値のバイアスが導かれる。この「間接推定法」により得られたバイアスを用いることで、実効増倍率の「測定値」よりもより高精度に、また、より高い信頼度で体系の未臨界度の推定が可能となる。
桜井 淳; 荒川 拓也*; 山本 俊弘; 内藤 俶孝
JAERI-Research 96-045, 31 Pages, 1996/08
JAERI-Research-96-045.pdf:0.87MB
「計算誤差間接推定法」では未臨界度予測精度は、
-
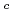=K(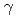
-
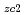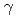
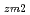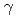
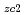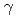
)で表される。この式は、未臨界度予測精度は軸方向のバックリングの予測精度である(-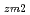)に比例することを意味している。比例定数Kは計算によって求めるが、Kの不確かさが未臨界度予測精度に与える影響は、直接=K(+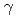
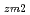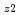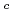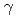
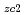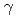
)によって求めた未臨界度と固有値計算によって求めたとを比べる場合に比べてはるかに小さい。したがってKの値は、既算の値を計算によって求めておけば精度は充分に保たれる。もし=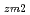であれば、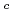=となる。TCAの四つの未臨界炉心の実験解析を基にこの方法の信頼性を示すことができた。
桜井 淳; 荒川 拓也*; 内藤 俶孝
JAERI-Research 96-008, 77 Pages, 1996/02
JAERI-Research-96-008.pdf:1.66MB
臨界集合体TCAを利用して7種類の未臨界炉心を構成し、反応度と中性子計数率空間分布を測定した。実験解析にはMCNP-4Aを利用した。中性子計数率空間分布の計算結果は、すべてその実測値と相互の誤差範囲内でよく一致している。このことは「計算誤差間接推定法」では、MCNP-4Aでの固有値問題の計算で求めた中性子増倍率は、その体系で実験的に評価した反応度から求めたものに一致することを意味している。今回の実験と計算によって「計算誤差間接推定法」を適用した計算値を用いた未臨界度の評価法の基礎技術を確立することができた。
内藤 俶孝; 荒川 拓也*; 桜井 淳
JAERI-Research 95-053, 24 Pages, 1995/07
JAERI-Research-95-053.pdf:0.85MB
「計算誤差間接推定法」による中性子増倍率の新しい評価法を提案する。第2章には「計算誤差間接推定法」の考え方及び中性子源増倍法への適用について、第3章には原研の臨界集合体TCAの実験データを基にこの方法の妥当性の検証について記述してある。連続エネルギーモンテカルロコードMCNP-4Aで計算した中性子増倍率にこの方法を適用し、得られた結果を指数実験法で評価した中性子増倍率と比較した。その結果、両者はよく合うことがわかった。
