Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
宮戸 直亮; 岸本 泰明; Li, J.
Physics of Plasmas, 11(12), p.5557 - 5564, 2004/12
被引用回数:118 パーセンタイル:94.60(Physics, Fluids & Plasmas)トカマクプラズマ中の電磁的イオン温度勾配駆動乱流-帯状流結合系を、グローバル電磁ランダウ流体コードを用いて調べた。帯状流の振る舞いは安全係数の大きさにより変化する。低安全係数領域では静的な帯状流が励起され、乱流を効果的に抑える。高安全係数領域では帯状流とポロイダル非対称な圧力揺動が結合し、帯状流が振動する。この振動帯状流のエネルギーがポロイダル非対称な圧力揺動を介して非線形的に乱流へ輸送されていることが同定された。このため、高安全係数領域では帯状流が乱流輸送を抑えることができない。帯状流の振る舞いの観点から、トカマクプラズマの閉じ込め改善には静的な帯状流が支配的となる低安全係数領域を作ることが好ましい。
佐々 成正
日本応用数理学会論文誌, 14(2), p.91 - 98, 2004/06
時間依存ギンツブルグーランダウ方程式は超伝導状態の時間発展を記述する方程式である。系の時間発展をシミュレーションするとき、ベクトルポテンシャルに対するマックスウェル方程式も同時に解くことが要求される。われわれはこのシステムを解く数値解法としてスプリッティング法を用いてその有効性を検証した。まず、このシステムに通常用いられている格子ゲージ理論を応用した差分スキームと比較して、われわれのスキームの方が数値安定性において優れていることを確認した。さらに、同様の計算精度を持ったRunge-Kutta法に対して、われわれの手法は必要な配列(メモリー)が少ないことが確認できた。これは計算が大規模になればなるほど重要となる特徴である。したがって、スプリッティング法は数値的に安定でかつ大規模問題に適した数値解法であることが、具体例を通して実証された。
佐々 成正; 町田 昌彦; 山田 進; 荒川 忠一
計算工学講演会論文集, 8(2), p.757 - 758, 2003/05
低温,磁場中での超伝導状態を記述するギンツブルグーランダウ方程式に代数的マルチグリッド(AMG)を適用し、数値シミュレーションを行った。AMGを用いる利点は主に次の2点である。まず、AMGを用いると大規模な問題が効率良く解けること。さらに、幾何学的マルチグリッドとは異なり、境界条件が複雑な場合でも適用可能であることが挙げられる。現実のシステムでは複雑な形状下でのシミュレーションを行わなくてはならないため、AMGの適用が不可欠である。これまでの研究では静的なギンツブルグーランダウ方程式の解法として最急降下法やCG法などの緩和法が数多く用いられてきた。本研究ではAMGと緩和法の計算効率についての比較をおこない、特定のパラメータ領域でAMGの優位性を示した。
佐々 成正; 町田 昌彦; 山田 進; 荒川 忠一
計算工学講演会論文集, 7(1), p.171 - 172, 2002/05
代数的マルチグリッド(AMG)を低温,磁場中での超伝導状態を記述するギンツブルグ-ランダウ方程式に適用し、これを数値的に解いた。AMGを用いる利点は主に次の2点である。まず、AMGを用いると大規模な連立1次方程式系を効率良く解けること。さらに幾何的マルチグリッドとは異なり、境界条件が複雑な場合にでも適用可能であることが挙げられる。現実のシステムでは複雑な形状下でのシミュレーションを行なわなければならないから、AMGの使用が不可欠である。通常ギンツブルグ-ランダウ方程式は緩和法で解かれることが多いが、AMGを使った方法の方が計算効率が良いことがわかった。
藤田 あゆみ
Physical Review B, 64(6), p.064504_1 - 064504_6, 2001/08
被引用回数:0 パーセンタイル:0.00(Materials Science, Multidisciplinary)磁場下での不純物を含む層状(2次元)超伝導体中で、ローレンツ力を受けて動いている磁束コア内の準粒子励起エネルギー準位の準位統計を調べる。磁束が移動する速度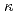 をさまざまに変化させた場合に、不純物濃度が異なる各相において数値計算によりユニバーサルな伝導度を求めた。速度が大きい場合に、ランダム行列理論の予測する結果と一致する結果を得た。反対に速度が小さい領域では、磁束芯内の不純物が1個というsuper-clean極限でのLarkin-Ovchinnikovの結果
をさまざまに変化させた場合に、不純物濃度が異なる各相において数値計算によりユニバーサルな伝導度を求めた。速度が大きい場合に、ランダム行列理論の予測する結果と一致する結果を得た。反対に速度が小さい領域では、磁束芯内の不純物が1個というsuper-clean極限でのLarkin-Ovchinnikovの結果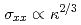 と一致する結果を得た。この場合、エネルギー散逸はエネルギー準位の間隔が平均のそれより非常に小さくなるいわゆる"avoided crossing"と呼ばれる場所でのLandau-Zener転移により起こると考えられる。
と一致する結果を得た。この場合、エネルギー散逸はエネルギー準位の間隔が平均のそれより非常に小さくなるいわゆる"avoided crossing"と呼ばれる場所でのLandau-Zener転移により起こると考えられる。
岩瀬 彰宏; 石川 法人; 岩田 忠夫*; 知見 康弘; 仁平 猛*
Physical Review B, 60(15), p.10811 - 10819, 1999/00
被引用回数:4 パーセンタイル:27.94(Materials Science, Multidisciplinary)熱分解黒鉛を35K以下で電子線照射し、磁気抵抗、ホール電圧を0-6Tの磁場下で、照射量の関数として測定した。測定結果をSimple Two Bandモデルを用いて解析し、以下のことがわかった。熱分解黒鉛の負の磁気抵抗は、電子に対してアクセプタとして働く格子欠陥、系の2次元性、欠陥によってブロードニングした2次元ランダウレベルの存在によって生じる。
内海 隆行*; 功刀 資彰; Koga, J. K.
Computer Physics Communications, 108(2-3), p.159 - 179, 1998/00
被引用回数:14 パーセンタイル:62.35(Computer Science, Interdisciplinary Applications)超強光電場でのプラズマの励起過程や緩和過程に伴う非線形現象が支配的な非局所熱平衡状態でのメゾスコピックな光量子-物質相互作用の研究においては、Boltzmann方程式の様な速度分布関数の運動方程式を数値的に精確に解くことが重要な要件となる。近年、矢部等により提案されたCIP法やそのラグランジュ表現のDA-CIP法といった数値解析技法は基本的には流体方程式などの双曲型偏微分程式に対する汎用解法として開発されてきた。このため、これらの手法は微視的現象を記述するBoltzmann方程式などを解く手法として直接的に適用できると考えられる。本論文では、DA-CIP法によりVlasov-Poisson方程式を位相空間において無衝突プラズマの不安定現象を解くことにより、この適用可能性を示す。
千原 順三
JAERI-M 5349, 72 Pages, 1973/07
Moriの連分数の方法を用いて、衝突を無視する近似とダイソン方程式のVertex partが移行運動量Qのみの関数であるとする近似をもとに一般化されたハートリー方程式を導いた。この方程式をもとに古典流体におけるオルンシュタイン=ゼルニケの関係式・直接相関関数を量子流体の場合に拡張した。この拡張は古典液体の動径分布関数g(r)にたいする積分方程式を導くpercusの方法の量子流体の場合への拡張を与える。この方法を用いて、中性および荷電量子流体のg(r)にたいする積分方程式を得た。これらの方程式を組みあわせることにより、一般化されたハートリー方程式はランダウ方程式・ランダウ=シリン方程式の大波数Q・高周波W領域かつ有限温度の場合の拡張を与えることが示される。さらに中性および荷電量子流体におけるg(r)・時空間相関関係G(r,t)・分布関数n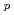 の3量を自己無撞着な形で、相互作用の強弱によらず、定める体系的な方法を与えた。
の3量を自己無撞着な形で、相互作用の強弱によらず、定める体系的な方法を与えた。
千原 順三
Progress of Theoretical Physics, 50(4), p.1156 - 1181, 1973/04
被引用回数:38Moriの連分数の方法を用いて導いた一般化されたハートリー方程式をもとに、古典液体におけるOrnstein-Zernikeの関係式、直接相関関数を量子液体の場合に拡張した。これをもとに、1つは外場中の電子ガスにたいするHokenberg-Kohn-Merminの理論を、一般の量子液体の場合に拡張し、1つは古典液体での積分方程式を導くPercusの方法を、量子液体の場合に拡張した。この方法を用いて中性量子液体にたいしてPercus-Yevickの方程式・Hypernetted chain方程式を拡張した。荷電量子液体(電子ガス)にたいしては、相互作用を短い部分と長く弱い部分に分けることにより、新しい積分方程式を導いた。中性および荷電量子液体にたいするこれらの方程式と組みあわせると、一般化されたハートリー方程式は、それぞれフェルミ液体におけるLandau方程式、電子ガスにたいするLandau-Silin方程式の、大きな波数、周波数領域への拡張を与えていることが示される。