Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
玉井 広史; 石田 真一; 栗田 源一; 白井 浩; 土屋 勝彦; 櫻井 真治; 松川 誠; 逆井 章
Fusion Science and Technology, 45(4), p.521 - 528, 2004/06
被引用回数：0 パーセンタイル：0.00(Nuclear Science & Technology)非定常1.5次元プラズマ輸送解析コード(TOPICS)を用いて、JT-60を超伝導化する改修装置(JT-60SC)における中心電流ホールつき非誘導電流駆動プラズマの時間発展を模擬した。JT-60Uの負磁気シア配位における実験結果から導かれた熱・粒子輸送係数を磁気シアの函数として与えて解析し、プラズマ電流1.5MA,トロイダル磁場2T,95%の磁気面における安全係数(q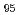
)4.5で閉じ込め改善度(HH
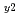)が約1.4,規格化ベータ値(
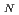)が3.7,自発電流割合が約75%の非誘導完全電流駆動プラズマにおいて電流ホールが小半径の約30%の領域まで達したプラズマを、約60秒と、ほぼ定常に維持できることを示した。また、電流ホールつき定常プラズマを得るには、自発電流及び内部輸送障壁の形成領域と電流ホールの位置関係が重要であることが示唆されている。得られたプラズマ分布をもとにMHD解析コード(ERATO-J)によってプラズマの安定性を評価した結果、導体壁をプラズマ近傍に設置することにより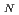の限界が4.5まで上昇することが示された。
徳田 伸二; 相羽 信行*
Journal of Plasma and Fusion Research SERIES, Vol.6, p.207 - 209, 2004/00
ニューコム方程式の研究の最新の進展について報告する。主として、高nキンクモードであるピーリングモードも含んだ外部モードの解析について述べる。また、低nモードについては、抵抗性壁モードの解析にも有用な理論を展開した。
徳田 伸二
Proceedings of 30th EPS Conference on Controlled Fusion and Plasma Physics (CD-ROM), 4 Pages, 2003/00
二次元Newcomb方程式に随伴する固有値問題を解くことにより、理想MHD的な摂動に対するトカマクプラズマの安定性を判定することができる。この固有値問題は、不安定なプラズマに対する成長率を与えない。しかし、成長率と固有値の間の関係を与える分散関係式を構築でき、それによって、成長率を決定することができる。分散関係式は理想MHD的な摂動に対して臨界安定に近いMHDモードの安定性を解析するための効果的な、かつ、高速な方法を提供し、かつ、臨界安定に近い場合の非理想MHDモードに対し拡張できると期待される。
徳田 伸二
Nuclear Fusion, 41(8), p.1037 - 1045, 2001/08
被引用回数：14 パーセンタイル：40.11(Physics, Fluids & Plasmas)トカマクの理想及び抵抗性MHD安定性解析のための、より進んだ漸近線接続法を報告する。まず、2次元Newcomb方程式を解く固有値問題法を論じる。この方法から得られる固有関数を外部解に利用できることを示し、不安定な理想MHDモードの線形成長率を求める分散関係式をはじめて導く。これまで、抵抗性MHD内部層方程式を初期値問題として解くことができなかったが、この問題を解く新しいスキームを提案し、その有効性を数値実験によって示す。
徳田 伸二
Journal of Accelerator and Plasma Research, 5(1), p.87 - 108, 2000/00
トカマクにおける2次元Newcomb方程式に随伴する新しい固有値問題を導き、それを数値的に解いた。固有値問題の定式化では、重み関数と境界条件を固有値問題のスペクトルが実の可算個の固有値(点スペクトル)だけからなり、連続スペクトルをもたないように選んだ。本定式化はいくつかの著しい特徴をもつ。まず、この定式化により理想MHD的に安定な状態を特定できる。次に、抵抗性MHD安定性理論において本質的な役割をはたす外部領域接続データを、理想MHD的に臨界安定に近い場合にも計算することができる。
徳田 伸二; 渡辺 朋子*
Physics of Plasmas, 6(8), p.3012 - 3026, 1999/08
被引用回数：58 パーセンタイル：83.31(Physics, Fluids & Plasmas)トカマクのような軸対称トロイダルプラズマにおける2次元ニューコム方程式の新しい固有値問題を提示する。この定式化においては、固有値問題のスペクトルが可算無限個の実数の固有値(点スペクトル)のみからなり、連続スペクトルを持たないように、重み関数(運動エネルギー積分)と有理面における境界条件とを設定した。理想m=1モードへ適用し、本定式化が不安定状態のみならず、安定状態も特定できること、及び、数値的に得られた固有関数が有理面で理論的に予想される特異性を示すことを実証した。
徳田 伸二; 渡辺 朋子*
統計数理研究所共同研究リポート, 110, p.70 - 77, 1998/03
トカマクプラズマ配位における2次元Newcomb方程式に随伴する固有値問題を提案する。この定式化においては重み関数(運動エネルギー積分)と有理面における境界条件を適切に選び、固有値問題のスペクトルが実可算の固有値(点スペクトル)だけから成り、連続スペクトルを持たないようにした。この定式化によって理想磁気流体力学的運動に対して、不安定状態だけでなく安定状態の特定が可能となった。
p mode plasmas in the Japan Atomic Energy Research Institute Tokamak-60 upgrade竹治 智; 鎌田 裕; 小関 隆久; 石田 真一; 滝塚 知典; 閨谷 譲; 徳田 伸二
Physics of Plasmas, 4(12), p.4283 - 4291, 1997/12
被引用回数：16 パーセンタイル：49.40(Physics, Fluids & Plasmas)高ポロイダルベータ(p)モードは、内部輸送障壁に起因する閉じ込め改善モードである。内部輸送障壁は、その内側の閉込め特性を著しく改善する一方で、その近傍で強い圧力勾配を形成するために、局所的な不安定性の原因となることが分かってきた。このことは、プラズマ内部の局所的な圧力・電流分布がプラズマ安定性に極めて重要であることを示している。本論文では、内部輸送障壁近傍に局在する不安定性(BLM)の実験解析・数値解析を行い、その発生機構の解明を試みた。実験解析の結果は、BLMが局在した理想低トロイダル数(n)キンクモードであることを示唆した。MHD安定性数値解析の結果、内部輸送障壁による局所的な圧力勾配とそれに伴うブートストラップ電流の効果により、内部輸送障壁近傍に局在する理想低nキンクモードが存在し得ることを発見した。これらにより、BLMを同定しその発生機構を解明した。
徳田 伸二; 渡邉 朋子*
JAERI-Data/Code 97-040, 105 Pages, 1997/10
JAERI-Data-Code-97-040.pdf:2.32MB
トカマクのような2次元軸対象トロイダルプラズマの磁気流体力学的(MHD)安定性解析において重要な役割を果たす2次元Newcomb方程式の新しい解法を考案し、それに基づくコード(MARG2D)を開発した。新しい解法では2次元Newcomb方程式を固有値問題として解く。この際、固有関数が有利面における小さい解と正則解を正しく捉えるように重み関数(運動エネルギー積分)と有理面における境界条件を選定し、従来の困難を克服した。このコードを使うことにより、2次元配位における理想MHDモードの臨界安定状態の同定が可能になる。また、このコードは抵抗性MHD安定性解析において外部領域接続データを計算する上で不可欠である。従来の理想MHDコードERATOJとのベンチマークテストにより、MARG2Dコードで安定状態及び臨界安定状態が同定できることを実証した。
徳田 伸二; 熊倉 利昌*; 吉村 更一*
JAERI-M 93-075, 32 Pages, 1993/03
確定特異点を持つ常微分方程式の接続データを有限要素法で求めるPletzer-Dewarの方法をモデル方程式を用いて調べた。接続データは磁場閉じ込めプラズマの非理想MHD安定性解析で重要な役割をはたす。Pletzer-Dewarの方法では「大きい解」、すなわち確定特異点で二乗可積分でない基本解のフロベニウス級数が使われる。この有限要素法で得られる接続データの収束率、および、フロベニウス級数を有限項で打ち切ることが計算結果に与える影響について調べた。この研究の結果、有限要素法は接続データを高精度で求める有効な方法であることが示された。
徳田 伸二; 竹田 辰興
応用数理, 2(4), p.298 - 316, 1992/12
MHD(磁気流体力学)モデルにもとづく数値解析は制御核融合研究において、実験解析や装置のデザインの不可欠な手段として重要な役割をはたしている。この論文では核融合炉として最も有力な候補であるトカマクに閉込められたプラズマのMHD平衡と安定性の解析のためのモデルと数値的な手法について解説する。安定性については線形理想MHD系のスペクトル解析について詳しく述べるとともに、抵抗性MHD安定性問題についても簡単にふれる。物理的な結果よりもMHD系の特殊性を反映する数値解析上の問題点の解説に重点をおいた。
小関 隆久; 安積 正史; 鎌田 裕; 芳野 隆治; 徳田 伸二; 常松 俊秀; 永島 圭介; 吉田 英俊; 永見 正幸
Nuclear Fusion, 31(1), p.51 - 60, 1991/00
被引用回数：8 パーセンタイル：41.01(Physics, Fluids & Plasmas)JT-60におけるペレット入射プラズマについて、理想高nバルーニングモードと低nキンクモードの安定性について解析した。ペレット入射プラズマは、q=1有理面の内側で強くピークした圧力分布を持っている。ペレット入射時に観測された圧力勾配は、q=1面のすぐ内側で理想高nバルーニング限界に達している。この磁気面で限界値に達した後、限界近く安定な磁気面はq=1面内で広がる。しかし、q=1面内のポロイダルベータ
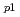は、理想バルーニングモードで制限される値に達していない。低nキンクモードの計算結果と実験的に観測された値を解析すると、実験的に達成した最大の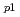は、n=1内部キンクモードによる限界値と一致する。
徳田 伸二; 山極 満; 常松 俊秀; 竹田 辰興
Int. Conf. on Plasma Physics, p.925 - 928, 1989/00
新古典効果(新古典抵抗およびブートストラップ電流)を無矛盾にとり入れたトカマク・プラズマの理想MHD安定性を解析する。この時、核融合の出力パワーを確保するためにITER計画で採用されたピークした密度・温度分布をもつ平衡を考え、そのような平衡に対する高-nバルーニング・モードおよび低-nモードに対するベータ値限界を解析する(n:トロイダル・モード数)。また粒子ビームによる電流駆動の解析モデルを平衡コードに取り入れて電流分布制御によるベータ値限界の改善についても調べる。
W.Kerner*; 徳田 伸二
JAERI-M 87-130, 26 Pages, 1987/08
定常流をもつ理想MHD平衡を表わす方程式を再吟味し自由プラズマ境界をもつトカマク配位の問題を数値的に扱った。
