Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
藤井 大輔; 中山 勝政*; 鈴木 渓
Physics Letters B, 868, p.139758_1 - 139758_6, 2025/09
リフシッツ公式は、有限温度におけるカシミール効果を解析するための基本的な理論枠組みとして広く知られている。本研究では、この公式を有限化学ポテンシャルのもとでの量子場に由来するカシミール効果へと拡張する。得られた一般化された公式の有用性を示すために、境界条件の違いや有限温度、空間次元の一般化、化学ポテンシャルの不均衡など、さまざまな設定における典型的なカシミール効果の特徴を検討する。この枠組みは、密なクォーク物質やディラック/ワイル半金属といった系にも適用可能であり、そこでは化学ポテンシャルがカシミール効果を制御するための調整パラメータとして機能する。
藤井 大輔; 中山 勝政*; 鈴木 渓
Physical Review D, 112(3), p.034020_1 - 034020_17, 2025/08
被引用回数：0磁場中の有限密度物質において、ディラックフェルミオンに由来するカシミール効果を理論的に解析する。特に、強い相互作用をもつディラック系における不均一な基底状態の候補として知られる「磁気二重カイラル密度波(MDCDW)相」におけるクォーク場に注目する。この相では、化学ポテンシャル・外部磁場・基底状態の空間的変調が複雑に干渉することで、カシミールエネルギーが距離に対して非自明な振動的挙動を示す。全カシミールエネルギーをランダウ準位ごとに分解することで、最低準位と高次準位のどちらが寄与するかによって、異なるタイプのカシミール効果が現れることが明らかになる。さらに、アップクォークとダウンクォークといったフェルミオンのフレーバー間の準位分裂に起因する特徴的な振る舞いも指摘する。
藤井 大輔; 川口 眞実也*; 田中 満*
Physics Letters B, 866, p.139559_1 - 139559_7, 2025/07
被引用回数：4 パーセンタイル：95.79(Astronomy & Astrophysics)我々は、スカーミオンを用いたスケール不変カイラル摂動理論に基づく枠組みにおいて、核子内部の閉じ込め圧力と、それに関連する重力形状因子であるD項を調査する。このアプローチでは、核子は量子化されたソリトンとして現れ、スケール対称性の破れは、低エネルギー定理に従ってスカラーメソン場をスケール異常に結合させることで効果的に取り入れられる。基礎理論であるQCDとの対応付けを通じて、スケール対称性の明示的および異常による破れは、それぞれパイオン質量とスカラーメソン質量を通じて記述される。核子のエネルギー運動量テンソルを分解することで、スケール異常の各成分が内部圧力にどう寄与するかを明らかにする。その結果、グルーオンによるスケール異常が閉じ込め圧力を支配していることが示される。従来のカイラル摂動理論のカイラル極限での結果と比較して、本研究の全体的な圧力分布はラティスQCDの結果とより良く一致している。さらに、グルーオン異常による圧力は広い空間領域にわたって分布しており、D項への顕著な寄与をもたらす。
藤井 大輔; 岩中 章紘*; 田中 満*
Physical Review D, 110(9), p.L091501_1 - L091501_8, 2024/11
被引用回数：8 パーセンタイル：85.74(Astronomy & Astrophysics)トップダウンのホログラフィック量子色力学(QCD)アプローチから、パイ中間子の重力形状因子(GFF)を運動量移動依存性を含めて初めて計算した。ハドロンのGFFは内部応力分布に関する情報を持っており、QCDがハドロンを形成するメカニズムの解明につながる可能性があるため重要である。このGFFsの前方極限値、すなわちD項も得られた。さらに、このアプローチでは、パイ中間子が無限個のグルーボールスペクトルを介して重力相互作用をする、いわゆるグルーボールドミナンスを観測した。
藤井 大輔; 中山 勝政*; 鈴木 渓
Physical Review D, 110(1), p.014039_1 - 014039_15, 2024/07
被引用回数：4 パーセンタイル：61.97(Astronomy & Astrophysics)カシミア効果は、微小体積に閉じ込められた光子場から誘起されることが知られており、また、そのフェルミオン的な対応物も、幅広い量子系で予言されている。ここでは、薄い有限密度クォーク物質において、どのような種類のカシミア効果がクォーク場から起こりうるかを調べる。特に、有限密度クォーク物質の基底状態の候補である二重カイラル密度波において、カシミアエネルギーが物質の厚さの関数として振動することを見いだした。この振動するカシミア効果は、Weyl半金属におけるカシミア効果と類似しており、クォーク場の運動量空間におけるWeyl点に起因すると考えることができる。さらに、クォークのフェルミ海からも振動が誘起され、全カシミアエネルギーは複数の振動の重ね合わせから構成されることを示す。
服部 恒一*; 末永 大輝*; 鈴木 渓; 安井 繁宏*
Physical Review B, 108(24), p.245110_1 - 245110_11, 2023/12
被引用回数：2 パーセンタイル：22.80(Materials Science, Multidisciplinary)通常の近藤効果は、伝導電子と交換相互作用を行う不純物を含んだ金属中で起こり、伝導電子のフェルミ面の存在が重要となるが、フェルミ面を持たない系における類似した現象の解明は近藤効果の基礎的理解のために重要である。さらに、通常の近藤効果は磁場中で抑制されるが、とある条件の下では磁場によって増幅することも起こりえる。本論文では、フェルミ面を持たない系において強磁場の存在に起因する近藤効果を記述するための模型を構築・提案する。この模型では、物質中を伝導するディラック粒子と物質内部で局在する不純物から成る粒子対である「近藤凝縮」を平均場として仮定することで、それを秩序変数とする相図を決定することができる。一方で、ディラック粒子・反粒子の粒子対として定義される「カイラル凝縮」は、クォーク系においては古くから知られた基底状態であるが、相互作用するディラック電子系においても類似した基底状態の存在が期待されている。さらに、ディラック粒子・反粒子間に極小の引力相互作用さえあれば、磁場の大きさに伴ってカイラル凝縮が(一般的には)増幅する現象が知られており、magnetic catalysis(磁気触媒機構)と呼ばれている。このため、本研究ではカイラル凝縮と近藤凝縮との磁場中での競合効果に注目し、この競合効果によって磁場をパラメータとする相図上に量子臨界点が現れることを予言した。さらに、磁場だけでなく有限温度の相図の予言も行った。フェルミ面に起因する通常の近藤効果とは異なり、強磁場のみによって誘起される近藤系はモンテカルロ法における負符号問題を持たないため、モンテカルロシミュレーションによって将来的に高精度の検証がなされることが期待される。
Kim, Y.*; 岡 眞; 末永 大輝*; 鈴木 渓
Physical Review D, 107(7), p.074015_1 - 074015_15, 2023/04
被引用回数：8 パーセンタイル：69.85(Astronomy & Astrophysics)重いクォークを1個含むバリオンは重クォークとダイクォークの束縛状態として記述できる。本研究では、ダイクォークのカイラル有効理論に基づき、ダイクォーク間のパイオン結合による遷移を模型化して、重バリオンの崩壊確率に関する研究を行った。
服部 恒一*; 末永 大輝*; 鈴木 渓; 安井 繁宏*
EPJ Web of Conferences, 276, p.01015_1 - 01015_5, 2023/03
被引用回数：0 パーセンタイル：0.00(Physics, Atomic, Molecular & Chemical)本研究では、重い不純物クォークを含む強磁場中のQCD相図を調べ、特に、平均場解析の範囲でこの系の基底状態を決定した。本研究で扱う模型の基底状態は、軽いクォークとその反クォークの対として構成される「カイラル凝縮」と軽いクォークと重いクォークの対である「近藤凝縮」の二種類の秩序変数によって特徴付けられる。強磁場中のQCDではカイラル凝縮が磁場に依存して増加するmagnetic catalysis (磁気触媒効果)と呼ばれる現象が知られているが、本研究では二種類の凝縮が相関・競合することで誘起される新たな現象として、カイラル凝縮の大きさが磁場の大きさに依らずに一定の値となる(飽和する)現象や、温度の増加に伴ってカイラル凝縮が特異的に増加する現象などを提案した。
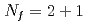lattice QCD with chiral fermions青木 慎也*; 青木 保道*; 深谷 英則*; 橋本 省二*; 金森 逸作*; 金児 隆志*; 中村 宜文*; Rohrhofer, C.*; 鈴木 渓
Proceedings of Science (Internet), 396, p.332_1 - 332_7, 2022/07
高温QCDにおける軸性U(1)異常の振る舞いはQCDの相図を理解するために重要である。JLQCD Collaborationによる以前の研究では、ドメインウォール・フェルミオンや(再重み付け法によって得られる)オーバーラップ・フェルミオンのような動的なカイラルフェルミオンを用いて2フレーバーQCDの高温相のシミュレーションを行った。本研究では、このシミュレーションを2+1フレーバー動的クォークを含む系へと拡張する。ここで、アップ、ダウン、ストレンジクォークは物理点近傍の質量をとし、2+1フレーバーQCDの擬臨界温度近傍、あるいはやや高い温度でシミュレーションを行う。本講演では、このシミュレーションから得られたディラックスペクトル、トポロジカル感受率、軸性U(1)感受率、ハドロン相関関数の結果を報告する。
青木 慎也*; 青木 保道*; 深谷 英則*; 橋本 省二*; Rohrhofer, C.*; 鈴木 渓
Proceedings of Science (Internet), 396, p.050_1 - 050_9, 2022/07
量子色力学(QCD)の黎明期においては、グルーオン場のトポロジカルな励起を通して軸性U(1)異常が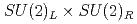
カイラル対称性の破れのトリガーとなることが期待されていた。しかし、そのような効果を格子シミュレーションを用いて定量的に検証することは近年まで困難であった。本研究では、格子上でのカイラル対称性を厳密に保つフェルミオン定式化を用いて、QCDの高温領域の数値シミュレーションを行った。このシミュレーションでは、格子上のカイラル対称性が満たされていることにより、スカラーおよび擬スカラーチャネルの感受率の中から軸性U(1)対称性の破れに起因する寄与を分離することが可能となる。2フレーバーQCDにおける結果は、
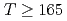MeVの温度領域におけるカイラル感受率が、軸性U(1)対称性の破れによって支配されていることを示唆している。
Kim, Y.*; 岡 眞; 鈴木 渓
Physical Review D, 105(7), p.074021_1 - 074021_17, 2022/04
被引用回数：37 パーセンタイル：95.13(Astronomy & Astrophysics)重いクォークを二個含むテトラクォーク(ダブルヘビーテトラクォーク)は深い束縛状態として存在する可能性があり、理論的・実験的に昔から注目されてきた。さらに、残りの二個の軽い反クォークはダイクォーク構造が発達している可能性があり、軽いクォークに寄与するQCD真空の理解に役立つという意味でも興味深い。本研究では、カイラル対称性を尊重した(軽い)ダイクォーク自由度を含むポテンシャル模型を用いて、ダブルヘビーテトラクォーク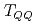
(
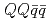、ただし、
, 
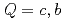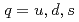)の質量スペクトルを調べた。特に、
, 
, 
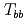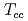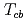テトラクォークを二個のヘビークォークと一個の反ダイクォークから構成される三体系として記述し、三体ポテンシャル模型を解くことにより質量スペクトルを求めた。この解析により、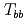は束縛状態として存在するが、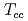と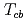は(深い)束縛状態として存在しないことを予言した。さらに、カイラル対称性が(部分的に)回復した状況における(ダイクォーク質量変化に伴う)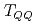テトラクォークの質量変化の予言も行った。
anomaly in the chiral susceptibility of QCD at high temperature青木 慎也*; 青木 保道*; 深谷 英則*; 橋本 省二*; Rohrhofer, C.*; 鈴木 渓
Progress of Theoretical and Experimental Physics (Internet), 2022(2), p.023B05_1 - 023B05_12, 2022/02
被引用回数：14 パーセンタイル：79.90(Physics, Multidisciplinary)量子色力学(QCD)におけるカイラル対称性の自発的破れに関する相転移(カイラル相転移)の秩序変数は「カイラル凝縮」であるが、これと関係した量として、カイラル凝縮をクォーク質量で一階微分して得られる「カイラル感受率」という量が知られており、カイラル相転移を示唆する量の一つとしてこれまでしばしば注目されてきた。しかし、カイラル凝縮やカイラル感受率は軸性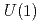対称性の破れとも関係しており、その詳細は未だ明らかでない。本論文は、相転移温度近傍におけるカイラル感受率の振る舞いを調べ、軸性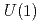対称性の破れがカイラル感受率にどのように寄与しているかを明らかにすることを目的とする。具体的には、カイラル感受率をディラック演算子の固有値分解を用いた形式で表すことにより、軸性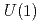対称性の破れと他の寄与を分離する手法を用いた。2フレーバー格子QCDシミュレーションの結果は、
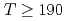MeVの温度領域におけるカイラル感受率が、軸性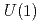対称性の破れに大きく支配されていることを示唆している。特に、connected partは軸性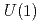感受率に、disconnected partはトポロジカル感受率と呼ばれる量によって支配されることが分かった。
石川 力*; 中山 勝政*; 鈴木 渓
Physical Review D, 104(9), p.094515_1 - 094515_11, 2021/11
被引用回数：7 パーセンタイル：41.75(Astronomy & Astrophysics)「ウィルソン・フェルミオン」と呼ばれる格子上のフェルミ粒子に対する近藤効果を記述する模型を構築し、様々な物理現象の予言・解明を行った。模型として、軽いウィルソン・フェルミオンと重いフェルミオンとの4点相互作用を含むカイラルGross-Neveu模型に対する平均場アプローチを用いた。結果として、ゼロ質量のウィルソン・フェルミオンからなる有限密度媒質において近藤効果が実現可能であることを示し、それに伴う近藤凝縮と軽いフェルミオン対の凝縮(スカラー凝縮)との共存相が存在可能であることを示した。このとき、スカラー凝縮が消える臨界的な化学ポテンシャルの値は近藤効果によってシフトする。さらに、負質量を持つウィルソン・フェルミオンにおいては、パリティ対称性が自発的に破れた相(Aoki phase)が生じることが知られているが、Aoki phaseが生じるパラメータ領域近傍で近藤効果も増幅されることを示した。本研究の発見は、ディラック半金属,トポロジカル絶縁体などの物質や、将来的な格子シミュレーションにおける不純物の役割を明らかにするために役立つことが期待される。
Kim, Y.*; Liu, Y.-R.*; 岡 眞; 鈴木 渓
Physical Review D, 104(5), p.054012_1 - 054012_18, 2021/09
被引用回数：19 パーセンタイル：72.60(Astronomy & Astrophysics)本論文では、スカラー及びベクトルダイクォークのカイラル有効理論を線形シグマ模型に基づいて構成する。有効理論の主な適用として、チャームまたはボトムクォークを1個含むシングルヘビーバリオンの基底状態と励起状態を記述する。ヘビークォーク(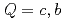
)とダイクォーク間の2体ポテンシャルを用いて、ヘビークォーク・ダイクォーク模型を構築し、
, 
, 
, 
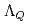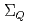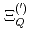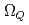バリオンの正パリティ及び負パリティ状態のスペクトルを求める。ここで、有効理論に含まれる質量や相互作用パラメータは、格子QCDから得られたダイクォーク質量やヘビーバリオンの実験値を用いて決定される。結果として、擬スカラーダイクォーク質量の逆ヒエラルキーに起因して
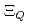(フレーバー
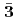)の負パリティ励起状態のスペクトルが、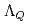とは異なる振る舞いを示すことを示す。一方で、
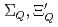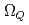, (フレーバー
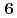)のスペクトルは、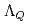と同様である。さらに、我々のヘビークォーク・ダイクォーク模型による結果と実験値やクォーク模型による結果との比較を議論する。
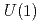anomaly at high temperature with lattice chiral fermions青木 慎也*; 青木 保道*; Cossu, G.*; 深谷 英則*; 橋本 省二*; 金児 隆志*; Rohrhofer, C.*; 鈴木 渓
Physical Review D, 103(7), p.074506_1 - 074506_18, 2021/04
被引用回数：31 パーセンタイル：85.78(Astronomy & Astrophysics)本研究では、格子QCDシミュレーションを用いて190-330MeVの温度領域における2フレーバーQCDの軸性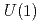アノマリーの性質を調べる。厳密なカイラル対称性を保つための格子フェルミオンとして、メビウス・ドメインウォール・フェルミオンや再重みづけ法によって構成されるオーバーラップ・フェルミオンを採用する。格子間隔は先行研究より小さい0.07fm程度であり、有限体積効果を正しく制御するために複数の体積でシミュレーションを行う。測定量として、トポロジカル感受率,軸性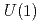感受率,メソン/バリオン相関関数における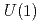パートナー間の縮退などの振る舞いを見る。臨界温度以上のすべての結果は、軸性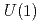対称性の破れが統計誤差の範囲でゼロと無矛盾であることを示唆している。クォーク質量依存性の結果は、
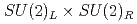カイラル対称性の破れと同程度に軸性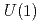対称性が回復していることを示唆している。
Rohrhofer, C.*; 青木 保道*; Cossu, G.*; 深谷 英則*; Gattringer, C.*; Glozman, L. Ya.*; 橋本 省二*; Lang, C. B.*; 鈴木 渓
Proceedings of Science (Internet), 363, p.227_1 - 227_7, 2020/08
量子色力学(QCD)の高温領域における性質は、カイラル対称性に関するクロスオーバー温度近傍において劇的に変化し、これまでに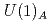
感受率,トポロジカル感受率,メソンスペクトルなどの物理量が調べられてきた。加えて、そのような高温領域における(核子などの)バリオンスペクトルの性質は、そのパリティ二重項構造に関連して注目されてきた。本研究では、格子QCDの数値シミュレーションによって、バリオンスペクトルにおけるカイラル対称性や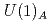対称性について調べる。ここでは、2フレーバーの動的なドメインウォール・フェルミオンを含むゲージ配位を用いて、臨界温度以上の高温相における体積依存性やクォーク質量依存性を検証する。さらに、高温相の相関関数においてemergentに現れる
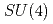対称性や
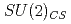対称性について議論を行う。
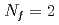lattice QCD鈴木 渓; 青木 慎也*; 青木 保道*; Cossu, G.*; 深谷 英則*; 橋本 省二*; Rohrhofer, C.*
Proceedings of Science (Internet), 363, p.178_1 - 178_7, 2020/08
本研究では、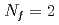の動的なメビウス・ドメインウォール・フェルミオンを含む格子QCDの数値シミュレーションによって、QCDの高温相における軸性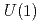対称性、オーバーラップ・ディラック演算子のスペクトル、メソン相関関数に対する遮蔽質量、トポロジカル感受率などの物理量を調べた。これらの中でいくつかの物理量は(格子上の)カイラル対称性の僅かな破れに敏感であるため、そのような物理量に対してはメビウス・ドメインウォール・フェルミオンからオーバーラップ・フェルミオンへの再重みづけを行った。さらに、有限体積効果を検証するために複数の体積でのシミュレーションも行った。T=220MeV以上の高温領域におけるカイラル極限(クォーク質量がゼロの極限)近傍の結果は、軸性U(1)異常の強い抑制を示唆している。
Kim, Y.*; 肥山 詠美子*; 岡 眞; 鈴木 渓
Physical Review D, 102(1), p.014004_1 - 014004_9, 2020/07
被引用回数：23 パーセンタイル：75.19(Astronomy & Astrophysics)カイラル対称性に基づく有効理論を、現象論的なクォーク模型の閉じ込めポテンシャルと組み合わせることにより、ヘビークォークを1子含むバリオンの質量や構造の予言をおこなった。とりわけ、ダイクォーク質量の逆ヒエラルキー効果がチャームおよびボトムバリオンの質量準位に反映されることを予言した。
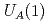anomaly原田 正康*; Liu, Y.-R.*; 岡 眞; 鈴木 渓
Physical Review D, 101(5), p.054038_1 - 054038_11, 2020/03
被引用回数：21 パーセンタイル：72.53(Astronomy & Astrophysics)カイラル対称性に基づく有効理論を用いて、ダイクォークおよびそれを含むヘビーバリオンの質量や構造の解析を行った。特に、有効理論における軸性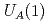アノーマリーの効果について新しい知見を得た。
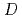mesons as a probe of Casimir effect for chiral symmetry breaking石川 力*; 中山 勝政*; 末永 大輝*; 鈴木 渓
Physical Review D, 100(3), p.034016_1 - 034016_14, 2019/08
被引用回数：7 パーセンタイル：34.33(Astronomy & Astrophysics)本論文では、ゼロ温度および有限温度におけるカイラル対称性の自発的破れに対する有限体積効果を検証するために、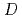中間子がプローブとして役立つことを示した。まず、2+1フレーバーの構成子クォークを含む線形シグマ模型を用いることで、
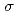平均場に対するCasimir効果を解析した。この解析では、反周期境界条件でカイラル対称性が回復し、周期境界条件で対称性の破れが増幅するという結果が得られた。さらに、有限温度・体積平面における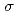平均場の相図を示した。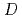中間子に対しては、カイラルパートナー構造に基づく有効模型を構築した。ここで、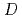中間子質量の体積依存性は、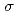平均場によって与えられる。
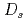中間子は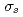
平均場を含むため、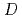中間子と比べて体積変化に対する応答が鈍いことが判明した。高温・周期境界条件においては、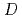中間子の質量シフトに異常が見られることを発見し、この振る舞いは将来の格子QCDシミュレーションによる検証で役立つことが期待される。さらに、コンパクト化空間次元の数の依存性も調べた。
