Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
佐々 成正
JSIAM Letters, 16, p.37 - 40, 2024/06
ハミルトン偏微分方程式系に対する数値的運動量保存則をシンプレクティック数値積分法を用いて考察した。非線形クラインーゴルドン系では、運動量がギリギリ保存する分散係数の臨界値が、全格子数の逆二乗に比例する事を示した。この結果は元の運動方程式の持つスケール普遍性からの帰結に矛盾しない。一方で、非線形シュレーディンガー方程式系の場合には分散係数の臨界値が運動方程式のスケール普遍性に一致していない事がわかった。
佐々 成正
Journal of the Physical Society of Japan, 91(5), p.054001_1 - 054001_8, 2022/05
被引用回数：1 パーセンタイル：15.48(Physics, Multidisciplinary)The validity of the interpolation method in the phase space is investigated in symplectic time integration of Hamiltonian systems. Theoretically, we show that the orbit of the interpolated point in the phase space coincides with the true orbit defined by Hamilton's equations of motion under restricted conditions using the discrete Fourier interpolation method. Even under general conditions, the interpolated point in the phase space evolves close to the true orbit. We conduct numerical simulations to demonstrate that our interpolation method, which approximates the true orbit, has sufficient numerical accuracy under general conditions.
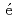integral invariant and conserved quantity of Toda lattice systems佐々 成正
JSIAM Letters, 14, p.88 - 91, 2022/00
Numerical properties of the Poincar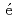 integral invariant of the Toda lattice systems are investigated based on the discrete Fourier interpolation method. In the 1D Toda lattice, we show that the Poincar 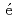integral invariant is conserved in a finite time interval in a symplectic time integration. In contrast, a conserved quantity of the 2D Toda lattice is conserved for a long time interval because of the interaction perpendicular to the lattice direction.
佐々 成正; 井上 純一*
東京大学工学教程; 基礎系数学,常微分方程式, 174 Pages, 2020/04
本書は、複雑現象シミュレーションのための基盤技術の研究開発に従い実施した計算手法に関する研究成果である。原子力工学を含む工学分野においてその基礎となっている常微分方程式に関する全般的な解説を行った。特に、境界値問題,連立微分方程式,定性的理論についての説明を行った。
佐々 成正
数理科学, 56(5), p.22 - 28, 2018/05
本発表は、材料研究開発支援のための高度基盤の研究開発に従い実施した計算手法に関する研究成果である。原子力工学を含む工学分野においてその基礎となっている微積分学に関する簡単な解説を行った。特に、空間次元が増えた場合に対し、スカラー,ベクトル場の概念や積分定理の概念についての説明を行った。
山田 進; 伊奈 拓也*; 佐々 成正; 井戸村 泰宏; 町田 昌彦; 今村 俊幸*
Proceedings of 2017 IEEE International Parallel & Distributed Processing Symposium Workshops (IPDPSW) (Internet), p.1418 - 1425, 2017/08
被引用回数：3 パーセンタイル：56.04(Computer Science, Hardware & Architecture)本発表では、BaileyのDouble-Doubleアルゴリズムを利用した4倍精度基本線形代数演算ライブラリ「BLAS」の高速化と、それを4倍精度固有値計算ルーチンに適用した際の計算性能の向上について発表する。特筆すべき成果は、積和演算の中間結果を高精度で保持して計算できるFMA命令を利用することで、我々がこれまでに開発した4倍精度BLASと比較し、代表的なルーチンで20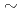
45%の高速化を実現したことである。さらに、4倍精度固有値ソルバ「QPEigenK」が利用している4倍精度BLASをFMA命令を利用して開発したものに置き換えるだけで、原子力機構のICE Xおよび東京大学のFX10の2つのスパコンの大規模並列計算において1020%の高速化を実現した。この成果は、計算機の大規模化に伴って必要になりつつある高精度計算の高速な実行に資する成果である。
integral invariant and momentum conservation in symplectic time integration of Hamiltonian partial differential equations佐々 成正
Journal of the Physical Society of Japan, 86(7), p.074006_1 - 074006_6, 2017/07
被引用回数：3 パーセンタイル：26.57(Physics, Multidisciplinary)ハミルトン系偏微分方程式の時間発展問題を考える。特に元の偏微分方程式系で運動量保存則が成り立っている時、時間発展手法にシンプレクティック数値積分法を用いると運動量保存則が数値計算においても保存されることを一般的に証明した。この証明には、ハミルトン系の相空間における保存則を満たすポアンカレ不変量(相空間におけるLouvilleの定理の最低次元版)を用いた。
佐々 成正; 山田 進; 町田 昌彦; 今村 俊幸*
Nonlinear Theory and Its Applications, IEICE (Internet), 7(3), p.354 - 361, 2016/07
フールエ変換を連続使用した場合の丸め誤差の累積誤差について議論を行った。偏微分方程式の数値計算において、フールエ変換を繰り返し連続使用した場合に丸め誤差が累積することを確認した。計算精度の毀損を補うため4倍精度高速フーリエ変換を用いた計算を行って有効性を確認した。
佐々 成正
Journal of the Physical Society of Japan, 83(12), p.123003_1 - 123003_4, 2014/12
被引用回数：4 パーセンタイル：33.24(Physics, Multidisciplinary)材料研究開発支援のための高度基盤の研究開発に従い実施した量子凝縮系非線形ダイナミクスに 対する並列シミュレーション計算手法に関する研究成果である。大規模並列計算における計算手法として、エネルギー保存、運動量保存を満たす陰的なシンプレクティック数値積分を考案し、その保存性能を理論的に検証した。また、数値シミュレーション実行時に計算の信頼性の指標となる保存則を実際の計算においてモニターし、従来手法よりも高精度を保つことを例証した。
佐々 成正
Journal of the Physical Society of Japan, 83(5), p.054004_1 - 054004_4, 2014/05
被引用回数：5 パーセンタイル：38.53(Physics, Multidisciplinary)本発表は、材料研究開発支援のための高度基盤の研究開発に従い実施した量子凝縮系非線形ダイナミクスに対する並列シミュレーション計算手法に関する研究成果である。大規模並列計算における計算手法として、エネルギー保存、運動量保存を満たす差分シンプレクティック数値積分を考案しその保存性能を検証した。特に、運動量保存則に対して、それが成り立つための条件を明らかにした上で、理論的な解明を行った。さらに計算の信頼性の指標となる保存則をモニターし、従来手法よりも高精度を保つことを実証した。
dinger-type equation佐々 成正
Journal of the Physical Society of Japan, 82(5), p.053001_1 - 053001_4, 2013/05
被引用回数：8 パーセンタイル：49.17(Physics, Multidisciplinary)本発表は、材料研究開発支援のための高度基盤の研究開発計画の下実施した量子凝縮系非線形ダイナミクスに対する並列シミュレーション計算手法に関する研究成果である。大規模並列計算における計算手法として、確率密度保存,エネルギー保存,運動量保存を満たす差分シンプレクティック数値積分を考案しその保存性能を検証する手法を新たに開発した。特に、運動量保存則に対して、それが成り立つための物理的条件を明らかにしたうえ、理論的説明も与えた。さらに計算の信頼性の指標となる保存則をモニターした結果を示し、従来手法よりも高精度を保つことを実証した。
佐々 成正; 町田 昌彦
Progress in Nuclear Science and Technology (Internet), 2, p.609 - 612, 2011/10
本論文は、液体ヘリウムを利用した高精度放射線検出装置開発に資することを目的とし、放射線により誘起される超流動乱流の動力学的性質や統計的性質を大規模数値シミュレーションした結果とその理論的考察により得られた結果を発表するものである。実施した大規模シミュレーション対象は、等方的な乱流状態であり、低波数にエネルギーを初期値として与え、その緩和をおもに観察した。その結果、発生し発達する量子渦の大規模乱流構造は、低波数領域では、通常流体乱流の渦構造と類似性を持つことが判明した一方、コルモゴロフ則が成立する慣性領域は、エネルギーカスケードの遅延によるボトルネック効果により通常乱流のものより狭くなることが確認された。これらの事実は、最近提唱され始めた超流動乱流の散逸ボトルネック効果を明らかに支持する結果であり、高精度に超流動乱流の特徴を明らかにした結果と位置付けられる。
佐々 成正; 叶野 琢磨*; 町田 昌彦; L'vov, V. S.*; Rudenko, O.*; 坪田 誠*
Physical Review B, 84(5), p.054525_1 - 054525_6, 2011/08
被引用回数：49 パーセンタイル：84.35(Materials Science, Multidisciplinary)本論文は、超流動における乱流現象を捉えた大規模シミュレーション結果とその理論的解釈を主題とした論文である。大規模シミュレーションは、超流動乱流の動力学的性質や統計的性質を解明するため、最大規模で2048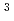
メッシュというサイズで実施され、おもに地球シミュレータを利用し実行されている。その結果、さまざまなサイズで測定されたスペクトルを比較することで、高波数側で超流動特有のエネルギー散逸が現れることを高精度に捉えることに成功し、2008年に提案されていたL'vov-Nazarenko-Rudenkoによる慣性領域に続いて現れるボトルネック効果を例証した。なお、本成果は、超流動乱流の理解という基礎研究上の一つの成果ではあるが、液体ヘリウムを利用した高精度な放射線検出器開発に対しても有用な知見を与える成果でもある。
町田 昌彦; 太田 幸宏; 佐々 成正; 小山 富男*; 松本 秀樹*
Journal of Physics; Conference Series, 248, p.012037_1 - 012037_8, 2010/11
被引用回数：9 パーセンタイル：90.22(Nanoscience & Nanotechnology)本発表では、異方性の高い高温超伝導体単結晶から発振されるテラヘルツ波発振についての理論的研究成果を発表する。発表では、まず、研究の背景、特に、実験から最近の理論的発展までの概略をレビューし、テラヘルツ波光源の重要性についても言及する。その後、当該研究グループでの理論及び数値シミュレーションによる成果を示し、最後にシミュレーションによる3次元アニメーション結果を報告する。
大谷 孝之; 佐々 成正; 清水 大志; 鈴木 喜雄
JAEA-Review 2007-009, 36 Pages, 2007/03
JAEA-Review-2007-009.pdf:2.74MB
システム計算科学センターにおいては、「独立行政法人日本原子力研究開発機構の中期目標を達成するための計画(中期計画)」に基づき、シミュレーション工学研究に関する研究開発を実施している。この研究開発の効率的・効果的推進に資することを目的として、機構外の有識者・専門家による研究評価及び示唆を受けるため、機構の原子力コード研究委員会の下に原子力計算科学研究評価専門部会が設置された。本報告は、平成17年度にシステム計算科学センターにおいて実施されたシミュレーション工学研究の実績を原子力計算科学研究評価専門部会が評価した結果をとりまとめたものである。
佐々 成正; 山田 進; 町田 昌彦; 荒川 忠一*
日本計算工学会論文集, 7, p.83 - 87, 2005/05
近年、幾何学的多重格子法(GMG)を改良した代数的多重格子法(AMG)が大規模連立一次方程式に対する高速ソルバーとして注目されている。われわれは磁場中での超伝導状態を記述するギンツブルグ-ランダウ方程式にこのAMGを適用して数値シミュレーションの高速化を行った。磁場中での問題であること、及び複雑な境界条件下での扱いが必要となるため、GMGではなくAMGの適用が必要不可欠である。本研究では、従来この問題の解法として用いられてきた共役勾配法とAMGの計算効率における比較によって、AMGの優位性を示した。
佐々 成正
日本応用数理学会論文誌, 14(2), p.91 - 98, 2004/06
時間依存ギンツブルグーランダウ方程式は超伝導状態の時間発展を記述する方程式である。系の時間発展をシミュレーションするとき、ベクトルポテンシャルに対するマックスウェル方程式も同時に解くことが要求される。われわれはこのシステムを解く数値解法としてスプリッティング法を用いてその有効性を検証した。まず、このシステムに通常用いられている格子ゲージ理論を応用した差分スキームと比較して、われわれのスキームの方が数値安定性において優れていることを確認した。さらに、同様の計算精度を持ったRunge-Kutta法に対して、われわれの手法は必要な配列(メモリー)が少ないことが確認できた。これは計算が大規模になればなるほど重要となる特徴である。したがって、スプリッティング法は数値的に安定でかつ大規模問題に適した数値解法であることが、具体例を通して実証された。
佐々 成正; 町田 昌彦; 山田 進; 荒川 忠一
計算工学講演会論文集, 8(2), p.757 - 758, 2003/05
低温,磁場中での超伝導状態を記述するギンツブルグーランダウ方程式に代数的マルチグリッド(AMG)を適用し、数値シミュレーションを行った。AMGを用いる利点は主に次の2点である。まず、AMGを用いると大規模な問題が効率良く解けること。さらに、幾何学的マルチグリッドとは異なり、境界条件が複雑な場合でも適用可能であることが挙げられる。現実のシステムでは複雑な形状下でのシミュレーションを行わなくてはならないため、AMGの適用が不可欠である。これまでの研究では静的なギンツブルグーランダウ方程式の解法として最急降下法やCG法などの緩和法が数多く用いられてきた。本研究ではAMGと緩和法の計算効率についての比較をおこない、特定のパラメータ領域でAMGの優位性を示した。
佐々 成正; 町田 昌彦; 山田 進; 荒川 忠一
計算工学講演会論文集, 7(1), p.171 - 172, 2002/05
代数的マルチグリッド(AMG)を低温,磁場中での超伝導状態を記述するギンツブルグ-ランダウ方程式に適用し、これを数値的に解いた。AMGを用いる利点は主に次の2点である。まず、AMGを用いると大規模な連立1次方程式系を効率良く解けること。さらに幾何的マルチグリッドとは異なり、境界条件が複雑な場合にでも適用可能であることが挙げられる。現実のシステムでは複雑な形状下でのシミュレーションを行なわなければならないから、AMGの使用が不可欠である。通常ギンツブルグ-ランダウ方程式は緩和法で解かれることが多いが、AMGを使った方法の方が計算効率が良いことがわかった。
佐々 成正
非線形派動現象のメカニズムと数理; 数理解析研究所講究録1209, p.188 - 193, 2001/05
シンプレクティック数値解法はハミルトン系に対する専用数値解法で系のエネルギーを(一定の幅の中で)保存する性質を持っている。さらに高次解法の実装が容易で例えば4次の解法は2次の解法を3回組み合わせて構成できる。同様に6次、8次の解法も2次の解法の組み合わせで実現される。このシンプレクティック数値解法を非線形波動方程式系に適用し高速で、高精度の数値解法の実相を目指す。具体的な適用例は非線形シュレーディンガー方程式やサインゴルドン方程式等の散逸の伴わない波動方程式系で、これらの系に対しては、ルンゲクッタ法等の従来の方法よりもはるかに計算効率の向上が確認できた。
